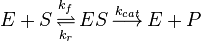Specificity constant
The specificity constant (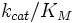 ), sometimes referred to as the kinetic efficiency, is a measure of the efficiency of an enzyme because the rate of the reaction directly varies with how frequently enzyme and substrate meet and how efficiently they bind in a solution. The specificity constant is a very useful kinetic value as it identifies the best substrate for a particular enzyme, in other words the specificity of an enzyme for a substrate.
The Michaelis dissociation constant (
), sometimes referred to as the kinetic efficiency, is a measure of the efficiency of an enzyme because the rate of the reaction directly varies with how frequently enzyme and substrate meet and how efficiently they bind in a solution. The specificity constant is a very useful kinetic value as it identifies the best substrate for a particular enzyme, in other words the specificity of an enzyme for a substrate.
The Michaelis dissociation constant ( ) reflects how well enzyme and substrate interact while the catalytic constant (
) reflects how well enzyme and substrate interact while the catalytic constant (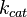 ) reflects the maximum rate of product formation (how fast the enzyme works). Since the maximum rate of product formation depends on how well the enzyme and substrate bind, its upper limit is the rate of enzyme and substrate binding (
) reflects the maximum rate of product formation (how fast the enzyme works). Since the maximum rate of product formation depends on how well the enzyme and substrate bind, its upper limit is the rate of enzyme and substrate binding (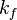 ). A kinetically perfect enzyme can bind its substrate at just below the rate of diffusion. By extension the upper limit of the catalytic constant is a little below the rate of diffusion (~108M-1s-1). A small
). A kinetically perfect enzyme can bind its substrate at just below the rate of diffusion. By extension the upper limit of the catalytic constant is a little below the rate of diffusion (~108M-1s-1). A small  reflects a tighter/better interaction between the substrate and enzyme. Therefore a large specificity constant reflects better enzyme efficiency.
reflects a tighter/better interaction between the substrate and enzyme. Therefore a large specificity constant reflects better enzyme efficiency.
In Michaelis-Menten kinetics the steady-state assumption is that [ES] formation equals [ES] destruction ( ). This assumption is made to make it easier to write a dissociation constant:
). This assumption is made to make it easier to write a dissociation constant: ![{\frac {[E][S]}{[ES]}}={\frac {k_{{r}}+k_{{cat}}}{k_{{f}}}}=K_{{M}}](/2014-wikipedia_en_all_02_2014/I/media/0/4/e/1/04e11a48732c4790732bcb00dec624b5.png) . The maximum velocity (
. The maximum velocity (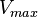 ) of an enzyme is the maximum product formation times the total concentration of enzyme available (
) of an enzyme is the maximum product formation times the total concentration of enzyme available (![V_{{max}}=k_{{cat}}[E_{{T}}]](/2014-wikipedia_en_all_02_2014/I/media/d/b/0/8/db0872105b21da4276a2d54343a793d9.png) ). The velocity of a reaction (
). The velocity of a reaction ( ) is the maximum velocity times the fraction of enzymes that are saturated (that are actually binding and converting substrate). The fractional saturation is equal to :
) is the maximum velocity times the fraction of enzymes that are saturated (that are actually binding and converting substrate). The fractional saturation is equal to :![{\frac {[S]}{K_{M}+[S]}}](/2014-wikipedia_en_all_02_2014/I/media/e/c/a/e/ecae20fa303217286d0a0e11d8e5f96a.png) . Consequently
. Consequently ![v=V_{{max}}{\frac {[S]}{K_{M}+[S]}}](/2014-wikipedia_en_all_02_2014/I/media/c/5/f/d/c5fdbd0300b3cb098c4d56774ab4e6d9.png) . We can now derive
. We can now derive ![v=k_{{cat}}[E_{{T}}]{\frac {[S]}{K_{{M}}+[S]}}](/2014-wikipedia_en_all_02_2014/I/media/7/3/9/c/739c6a3d09e69a6d9221b51153557a11.png) . From this equation one can write the most useful form of the Michaelis-Menten equation:
. From this equation one can write the most useful form of the Michaelis-Menten equation: ![{\frac {v}{[E_{{T}}]}}={\frac {k_{{cat}}}{K_{{M}}}}({\frac {[S]}{1+[S]}})](/2014-wikipedia_en_all_02_2014/I/media/e/4/0/6/e406a377f9e87e5adc7a79a1d3319ab6.png)
See
- Enzyme kinetics
- Michaelis-Menten kinetics
- turnover number.
References