Spatial acceleration

From Wikipedia, the free encyclopedia

In physics the study of rigid body motion provides for several ways of defining the acceleration state of a rigid body. The classical definition of acceleration entails following a single particle/point along the rigid body and observing its changes of velocity. In this article the notion of spatial acceleration is explored, which entails looking at a fixed (unmoving) point in space and observing the changes of velocity of whatever particle/point happens to coincide with the observation point. This is similar to the acceleration definition fluid dynamics where typically one can measure velocity and/or accelerations on a fixed locate inside a testing apparatus.

Definition

Consider a moving rigid body and the velocity of a particle/point P along the body being a function of the position and velocity of a center particle/point C and the angular velocity 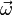${\vec \omega }$ .

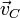The linear velocity vector ${\vec v}_{P}$ at P is expressed in terms of the velocity vector ${\vec v}_{C}$ at C as:

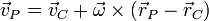
${\vec v}_{P}={\vec v}_{C}+{\vec \omega }\times ({\vec r}_{P}-{\vec r}_{C})$

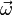where ${\vec \omega }$ is the angular velocity vector.

The material acceleration at P is:

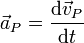
${\vec a}_{P}={\frac {{{\rm {d}}}{\vec v}_{P}}{{{\rm {d}}}t}}$

${\vec a}_{P}={\vec a}_{C}+{\vec \alpha }\times ({\vec r}_{P}-{\vec r}_{C})+{\vec \omega }\times ({\vec v}_{P}-{\vec v}_{C})$

where 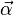${\vec \alpha }$ is the angular acceleration vector.

The spatial acceleration 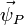${\vec \psi }_{P}$ at P is expressed in terms of the spatial acceleration 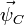${\vec \psi }_{C}$ at C as:

${\vec \psi }_{P}={\frac {\partial {\vec v}_{P}}{\partial t}}$

${\vec {\psi }}_{{P}}={\vec {\psi }}_{{C}}+{\vec {\alpha }}\times ({\vec {r}}_{{P}}-{\vec {r}}_{{C}})$

which is similar to the velocity transformation above.

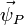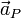In general the spatial acceleration ${\vec \psi }_{P}$ of a particle point P that is moving with linear velocity ${\vec v}_{P}$ is derived from the material acceleration ${\vec a}_{P}$ at P as:

${\vec {\psi }}_{{P}}={\vec {a}}_{{P}}-{\vec {\omega }}\times {\vec {v}}_{{P}}$

References

Frank M. White (2003). Fluid Mechanics. McGraw-Hill Professional. ISBN 0-07-240217-2. .
Roy Featherstone (1987). Robot Dynamics Algorithms. Springer. ISBN 0-89838-230-0. . This reference effectively combines screw theory with rigid body dynamics for robotic applications. The author also chooses to use spatial accelerations extensively in place of material accelerations as they simplify the equations and allows for compact notation.
JPL DARTS page has a section on spatial operator algebra (link: ) as well as an extensive list of references (link: ).
Bruno Siciliano, Oussama Khatib (2008). Springer Handbook of Robotics. Springer. . Page 41 (link: Google Books ) defines spatial accelerations for use in rigid body mechanics.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.