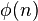Sparsely totient number

In mathematics, a sparsely totient number is a certain kind of natural number. A natural number, n, is sparsely totient if for all m > n,

φ(m)>φ(n),

where φ is Euler's totient function. The first few sparsely totient numbers are:

2, 6, 12, 18, 30, 42, 60, 66, 90, 120, 126, 150, 210, 240, 270, 330, 420, 462, 510, 630 (sequence A036913 in OEIS).

For example, 18 is a sparsely totient number because φ(18) = 6, and any number m > 18 falls into at least one of the following classes:

1. m has a prime factor p ≥ 11, so φ(m) ≥ φ(11) = 10 > φ(18).
2. m is a multiple of 7 and m/7 ≥ 3, so φ(m) ≥ 2φ(7) = 12 > φ(18).
3. m is a multiple of 5 and m/5 ≥ 4, so φ(m) ≥ 2φ(5) = 8 > φ(18).
4. m is a multiple of 3 and m/3 ≥ 7, so φ(m) ≥ 4φ(3) = 8 > φ(18).
5. m is a power of 2 and m ≥ 32, so φ(m) ≥ φ(32) = 16 > φ(18).

The concept was introduced by David Masser and Peter Shiu in 1986.

Properties

• If P(n) is the largest prime factor of n, then .
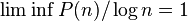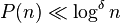• holds for an exponent .
• It is conjectured that .

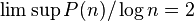References

• Baker, Roger C.; Harman, Glyn (1996). "Sparsely totient numbers". Ann. Fac. Sci. Toulouse, VI. Sér., Math. 5 (2): 183–190. ISSN 0240-2963. Zbl 0871.11060. 
• Masser, D.W.; Shiu, P. (1986). "On sparsely totient numbers". Pac. J. Math. 121: 407–426. ISSN 0030-8730. MR 819198. Zbl 0538.10006.