SpaceShaft

A SpaceShaft is a proposed Lighter than air (LTA), atmospherically buoyant, deep-draft, super-tall cylindrical-like structure that could serve as an elevator system for “Single-stage-to-orbit” vehicles (SSTO) to "near-space altitudes".

Important to distinguish from some other proposed Non-rocket spacelaunch systems (NRS) is that a SpaceShaft is neither; “a tower", (since, technically speaking, it is not standing on foundations or a surface, such as the surface of our planet,) nor it is a sub-set of the currently popular “Centrifugally Extended Carbon Nano Tube Tether Space Elevator” (CECNTTSE), since it is not stabilized, into the upright standing position, due to structural stiffening caused by centrifugal forces. Instead, metaphorically speaking, one can imagine a SpaceShaft as being like a giant, vertically floating, spar-buoy, (or spar platform also known as a oil platform). This vertically floating orientation is obtained by its anchoring to the ground ^[1] from its bottom end (or keel). While the cumulated buoyancy structurally stiffens the anchoring cables, which by a special distribution extend all the way up and so reaching up at it’s top end, or summit. The summit section supports a large enough flat surface, (with an average diameter of about 100 meters,) which is to serve as a Flight deck for the take-off or launching of the SSTOs. Typically the flight deck is located at a short altitude above an imaginary atmospheric (water) line representing the limit at which neutral buoyancy happens. The flight deck (or launching platform) could be well above the Troposphere.

Because of its design, (meant to cumulate buoyancy throughout the dense regions of the atmosphere and by using a special method of deployment which would be explained in a later section,) it would provide and transmit the gathered potential energy from the displaced atmospheric weight, (needed for its elevating movement and capacity,) following a First-In/First-Out (FI-FO) process. The reaction caused by the cumulated buoyancy and synchronized upward movement of the stacked sections been named upthrust and the representing formula is discussed later in the section named The upthrust formula.

Because of the significant weight displacement caused by the atmospheric column due to the regular increment of space occupancy, a SpaceShaft could be considered as capable of lifting super heavy cargo with estimated distributed capacities measured in thousands of tonnes. As for an example of such cargo; one can imagine the lifting of multiple units, (simultaneously,) of SSTOs, which are rockets especially designed for their use specifically above the troposphere and are to be launch horizontally, directly into a fly direction compatible with that of the path to their orbital flight, instead of the initially vertical flight which are typically used by multi-stage rockets, in which their first stages are dedicated to the exclusive task of lift-off, and precedes the typical second stages meant to achieving orbital velocities for near-space altitudes.

To carry out the elevation process, (of different payload types,) a SpaceShaft would use two separate and different methods of transportation, these are.

• The primary system which is characterized as being unidirectional and slow. However, it is the most efficient method for the lifting of heavy weights. This system would in fact be the LTA sections that make up the wall of the structure.
• While the secondary system will, (instead,) be bidirectional in nature and is to be used for the faster transport of lighter weight cargo or that of personnel. The secondary system would consist of a shuttle travelling trough the shaft and would be powered by a hybrid system of propulsion consisting of buoyancy and electro-mechanical crawlers.

As said before and to further elaborate upon its employment, a SpaceShaft would not be by itself able to launch its cargo into orbit. For the task of orbital insertions the elevated SSTO vehicles, (with their payloads,) must have their own (built-in) propulsion systems as to leave the carrying fly-deck and subsequently being individually capable of achieving the escape velocities which are needed as to enter their destination orbits.

General appearance and arrangement

The SpaceShaft is, overall, a tethered balloon, formed in the shape of a long, narrow column.

The general structural appearance of a SpaceShaft is that of an upright standing telescopic system behaving as a typical oceanic spar-buoy or spar type oil platform; instead of being "mostly submerged in water and partially rising into the atmosphere", it is "mostly submerged in the planet’s atmosphere and partially rising out into the fringes of Space".

Although a SpaceShaft is also described as a structure, it is not a space tower because it does not stand on foundations in contact with the surface of the planet as to support compressive forces (see image of mode 3 stretching and compression) caused by weight.^[2] A SpaceShaft is not a space launch system, however, from a platform at the top of a SpaceShaft either spaceplanes or spacecrafts with built-in propulsion systems could be launched.^[3]

It would support multiple platforms distributed at several elevations that would provide habitation facilities for long-term human operations throughout the mid-atmosphere and near-space altitudes. A SpaceShaft is potential component in non-rocket spacelaunch systems.^[1][3]

Because of the large volumes of displaced air-mass resulting from the diameters of its multiple concentrically aligned, telescopic cylinders (stabilization shafts) and their different heights, thousands of tons of buoyancy would be harnessed, making it theoretically possible to support several permanent platforms at the top of each of the stabilization shafts on the outer rims and thousands of tonnes of upthrust on the cylinders at the core of the telescopic system (transportation shafts). The type of shafts and their intended uses are discussed later.

Within the conduit at the innermost transportation shaft (i.e. the flue), which would extend from near sea-level to the highest elevation, where a platform will be located, a special shuttling-cab(s), comparable to a vertically oriented air-ship, will travel up and down the system quickly carrying personnel and light cargo, first by means of buoyancy and afterward by electromechanical systems.

The location of the individual platforms, except for the one at the summit of the highest shaft, are mostly distributed at altitudes below the Mesosphere, and so allowing for long term human activities never before possible throughout the mid-atmosphere of our planet. The reason for the distribution is that the platforms (also known as mooring platforms) also serve as the attaching points for guy-lines similar to those used with sailing masts and guyed mast antennae.

The platform at the top of the innermost shaft, i.e. the one within the core of the telescopic system, will be able to reach altitudes around 100 km, and perhaps above depending on the intended operation, and so potentially provide the needed support for facilities to exercise important non-orbital space operations. The platform could even provide the facilities for initiating the “assisted launch” of a typical second stage rocket or spaceplane (see rockoon and balloon-launched self-stabilized rocket).

Besides its capability of supporting multiple platforms throughout the atmosphere, a SpaceShaft will also serve to house a more traditional elevator system consisting of a special shuttling-cab traveling through the flue of the core shaft. It is however important to note that this elevator system can be considered as just the secondary elevator system that a SpaceShaft can provide for reasons that will be explained later in the Deployment section.

Description of building blocks missing

The building blocks of the SpaceShaft are only described as lighter than air and rigid. There is no concrete description of how to build such a building block which must be much lighter than air at normal conditions. Gas balloons with a fixed frame may be one possibility, but then a space shaft is more or less the lower part of a Balloon-evator.^[4] One possible material to use is aerographene, as of March 2013, the least dense solid known.

Possible uses of a SpaceShaft

• Tourism destination with spectacular view
• Atmospheric observation station
• Communications platform
• The ultimate BASE jumping experience
• Solar power generation

Deployment and FIFO delivery

The FIFO deployment sequence is as follows; having one of the buoyant building blocks already anchored; some slack is then given to the anchor lines as to let it further rise, i.e.; in a controlled fashion and for a limited height, as much as to allow for enough space being made as to insert a new buoyant building block right underneath the first one. These building blocks are then firmly attached to each other and so becoming a unit with the understandably incremented buoyancy. The process is then repeated for as many times as is necessary, such that: when both the desired carrying capacity and desired altitude are achieved for the building block at the top of the stack, with whatever payload is contained, is then submitted for their relocations. And so is the FIFO sequence completed.

As said, the SpaceShaft is assembled using atmospherically buoyant building blocks. These building blocks consist of specifically engineered buoyant pressure vessels. Some of which are designed for high buoyancy and ballasting, while others are engineered for more specific structural purposes. However, all of these building blocks are characterized by being buoyant and having internal skeletons made from composite materials, and so making these units very strong, very light, modular, and maintainable, even when they have already been integrated into the buoyant structure and have reached high atmospheric altitudes. One interesting property of such a buoyant structure is that in the event of an accident only limited amounts of debris will fall back to the ground since most of the building blocks will remain atmospherically buoyant.

Other components of the system are not as buoyant or may not be buoyant at all, (e.g. anchor lines, winches, deck equipment, etc.). The design goal of the SpaceShaft is to construct a structure that is; "atmospherically buoyant from sea level up to altitudes of 50km". Higher altitudes are attained by transferring excess weight as compressive loads down the SpaceShaft.

The SpaceShaft will have net positive buoyancy which will necessitate anchoring it to the ground. Additionally, since the lower portion of the SpaceShaft is subject to atmospheric winds will therefore require mooring lines. To quickly differentiate the functionality of the systems; the anchoring system is to keep the SpaceShaft from freely flying away, while the mooring system is to counteract lateral wind forces that could toss around the structure. More about the combined effects of wind loads and upthrust is discussed later, under the section of "Heave and roll behavior" which would describe the similar of a spar-buoy on a waterway and on the section "Wind force and Coriolis", likewise for bending and deflection on the structure. Beside the two mentioned external control systems there is an electronically controlled, self-sufficient, ballasting system incorporated into every one of the buoyant building blocks.

As the SpaceShaft is constructed, the sum total of the buoyant forces of all the component rings is available to support the weight(s) of the elevated (elevating) platform(s) and payloads. Thus, as you add more component rings, you increase the load carrying capacity of the SpaceShaft.

The SpaceShaft structure is constructed with a larger number of concentric rings at the lower levels. The SpaceShaft structure is wider at the base, narrower at the top. The appearance of which resembles a telescoping device. Some of the SpaceShaft structures may resemble an elongated version of the Burj Khalifa, currently the tallest building at 828 m (2,717 ft).

While the total volume of the Burj Khalifa is not listed, the floor area is listed as 309,473 square meters. If we approximate floor height as averaging 3 meters then the volume is 928,419 cubic meters. At the bottom of the Burj Khalifa (sea level) the density of air is approximately 1.2 kilograms per cubic meter. At the top of the Burj Khalifa (828 meters) the density of air is approximately 1.1 kilograms per cubic meter. With a total displacement of 928,419 cubic meters, and considering the majority of the displacement is at the bottom, using 1.175 kg/m³ average density of displaced air, the available buoyancy is approximately 1,090 metric tons (less the mass of the SpaceShaft components). While the average density of the SpaceShaft components is unknown at this time, targeted values are in the range of 0.1 to 0.2 kg/m³. Using the higher density, a sea level based SpaceShaft of the size and shape of the Burj Khalifa could lift 905 metric tons. The Burj Khalifa represents a structure that is approximately 1% the size (height and volume) of a SpaceShaft.

Buoyancy and upthrust

By definition, buoyancy is a static upward force that acts on a single object of lower density than its surrounding environmen, such as is the case of wooden piece being immersed in a fluid, but in the case of a SpaceShaft it is the air of the environment. The buoyant force is equal to the weight of the fluid displaced and not that of the displaced object. If the upward buoyant force is greater than the mass of the object immersed, the object will float; this is referred to as positive buoyancy. If the mass of the object is exactly equal to the mass of the fluid displaced (that is, the average density of the object equals the density of the fluid), this will produce neutral buoyancy. An object that is heavier than the fluid displace exhibits negative buoyancy. In contrast to regular buoyancy, upthrust consist of the cumulated buoyancy, (which is the static aspect,) and the reactive movement, which is the kinetic aspect. Therefore, the sum of all the buoyancy from all the cross-sectional elements that make a SpaceShaft is informally called, (by the developers of the SpaceShaft,) as the upthrust of the system.

The upthrust formula

The total upthrust U_t of a SpaceShaft equals the payload that it can carry at its top while still being in a neutral floating state. The total upthrust is computed assuming that:

• the SpaceShaft’s cross sectional area S may vary in function of the altitude h: S = S(h)
• the SpaceShaft’s mass per unit length m (i.e. the consolidated mass of its structure) may vary in function of the altitude: m = m(h)

where the altitude h is defined as h = r–r₀ with r the distance of the Earth's center and r₀ the Earth's radius.

The net vertical upthrust per unit length acting upon the SpaceShaft at a given altitude h, is the summation of the difference between the upward buoyancy force B(h) and the downward weight force W(h).

For the case that the height of the shaft is not negligible compared to the radius of the Earth, the upthrust must also account for the upward centrifugal force C(h) due to the Earth's rotation;

Thus, the net vertical upthrust U(h) per unit length is U(h) = B(h) – W(h) + C(h) . The different composing forces are detailed below.

Upward buoyancy force

The buoyancy force B(h) per unit length of the SpaceShaft at a given altitude is computed as

B(h) = S(h) · ρ_a(h) · g(h)

in which ρ_a(h) is the air density and g(h) the gravitational acceleration defined by:

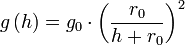
Since the height h of SpaceShaft is necessarily limited to the atmosphere, however, h will be much less than r_e, and hence g(h) can be approximated as constant (=g_o) to reasonable accuracy for most calculations

The buoyancy force here does not include the effect of the gas, if any, inflating the structure. This can be included in the weight. If it is included in the byoyancy force, the force is modified by making the effective density of the gas equal to the difference in density of the gas pressurizing the system from the density of the gas external to the system.

The buoyancy goes to zero as the altitude increases.

Downward weight force

The downward weight force per unit length is simply computed as:

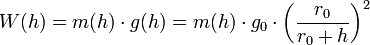
The total upthrust

The total upthrust U_t for a SpaceShaft with bottom section at an altitude h_b and top section at an altitude h_t is then given by the integration of the vertical upthrust U over the SpaceShaft's length. Neglecting centrifugal force (see next section), this is:

or, using the expressions for the respective upthrust components given above:

Considering a SpaceShaft that is in a neutral floating state (U_t = 0), the above expression in which h_t is replaced by any altitude between h_b and h_t gives the vertical buckling force the upper parts of the SpaceShaft exert on the lower parts of the SpaceShaft at that altitude. This allows to evaluate the vertical stresses in the internal of the SpaceShaft and, hence, to choose the appropriate materials and design to cope with these stresses.

In case the SpaceShaft is not in a neutral floating state (U_t > 0), the SpaceShaft must be anchored as discussed above. The anchoring force A(h_b) will then equal –U_t for the SpaceShaft to be in mechanical equilibrium. This force can then be used to evaluate the stresses in the anchoring system.

The total stress

If the weight of each segment at a given altitude is exactly equal to the buoyancy, there will be no stress on the structure (and the upthrust is zero). If the weight is greater or less than the buoyancy at a given altitude, then the material of the shaft must be carrying a load. For any of the structure significantly above the atmosphere, the buoyancy is zero, and hence the structure is in compression. The total compressional force can be computed by integrating (weight minus buoyancy) from the top of the tower downward. Stress can then be computed as the force divided by the cross sectional area at that point.

Simplification

In many cases the weight per unit length of the SpaceShaft will be proportional to its cross sectional area: m(h) = ρ_s · S(h) where ρ_s(h) is the SpaceShaft's own density. The total upthrust now becomes:

For a reasonable approximation, centrifugal force and the gravitational acceleration can be considered constant. The total upthrust is thus simply the buoyancy minus the weight:

Upward centrifugal force

Since the height h SpaceShaft is necessarily limited to the atmosphere, this term will be constant to a reasonable approximation, and thus the centrifugal force can simply be subtracted from the gravitational acceleration at the Earth's surface to give the effective gravity at the Earth's surface, go

For a more detailed calculation, the centrifugal acceleration due to the Earth's rotation is computed as:

in which ω_e is the constant Earth's rotation speed given by:

in which T_day is the duration of a day on Earth in seconds.

Since this term effectively reduces the effective gravity, it applies to both the weight and buoyancy force. Thus, the centrifugal force can be accounted for in the equations above by subtracting the centrifugal acceleration from the gravitational acceleration g_o

External Forces on the SpaceShaft

To cope with different lateral forces such as wind and Coriolis forces (for instance, when a shuttle is moving rapidly upward within the Spaceshaft), a number of stabilization techniques are envisaged that can be categorized in two main categories:

1. Passive techniques:
   • application of lightweight tensegrity like structures to enhance the stiffness of the SpaceShaft artefact
2. Active techniques:
   • spoke-like mooring systems at different altitudes (much like antenna-masts)
   • computer-controlled propeller nacelles at different altitudes to combat side winds

It is important to investigate how a SpaceShaft can remain in equilibrium under the effect of lateral forces in order to design appropriately the different aforementioned stabilization techniques. Mechanical equilibrium of the SpaceShaft is reached if the sum of all forces and the sum of all moments around some reference point (in this case the anchor point at the bottom of the SpaceShaft) are zero. In absence of any active stabilization technique, the SpaceShaft will no longer a straight vertical artefact but will have to lean against the side forces that are then compensation by the SpaceShaft's own weight force.

To model the mechanical static equilibrium of a SpaceShaft, the different acting forces and moments are listed below:

• the external forces : wind forces, Coriolis forces,...
• the SpaceShaft's own weight force
• the SpaceShaft's anchor force
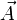
• mooring forces and/or propeller forces at discrete altitudes where i = 1,...,N with N the number of mooring stations or propeller nacelles; altitude increases with the index i;
• the moment 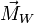generated by the external forces;
• the moment generated by the SpaceShaft's own weight;
• the moments generated by the mooring stations and propeller nacelles where i = 1,...,N with N the number of mooring stations or propeller nacelles;
• the moment caused by any possible bending of the SpaceShaft whose stiffness is resisting to such bending.

See also

• Space elevator
• Space fountain
• High-altitude platform

References

External links

Wikimedia Commons has media related to SpaceShaft.

• The SpaceShaft Endeavor
• The European Spaceward Association

v t e Non-rocket spacelaunch Spaceflight Static structures Compressive Space tower Pneumatic freestanding tower Tensile Skyhooks Space elevator Hypersonic skyhook SpaceShaft Bolus Rotovators Hypersonic bolus Other Endo-atmospheric tethers Dynamic structures Space fountain Orbital ring Launch loop Projectile launchers Electrical Coilgun Mass driver Railgun StarTram Chemical Space gun Blast wave accelerator Ram accelerator Mechanical Slingatron Reaction drives Air launch Spaceplanes Laser propulsion Beam-powered propulsion Buoyant lifting Balloon Buoyant space port Orbital airship High-altitude platform See also: Rocket sled launch Megascale engineering Category