Space–time tradeoff

In computer science, a space–time or time–memory tradeoff is a situation where the memory use can be reduced at the cost of slower program execution (and, conversely, the computation time can be reduced at the cost of increased memory use). As the relative costs of CPU cycles, RAM space, and hard drive space change—hard drive space has for some time been getting cheaper at a much faster rate than other components of computers^{[citation needed]}—the appropriate choices for space–time tradeoffs have changed radically. Often, by exploiting a space–time tradeoff, a program can be made to run much faster.

History

The basic idea of time–memory tradeoff goes back to the earliest time of evolution, since basically using knowledge instead of brute-force trials, and encoding reflex reactions in the DNA to avoid the organism to have to "calculate", i.e., think how to react, in time-critical situations, are examples of this. More specifically to the use in computers, look-up tables (and in particular, e.g., storing coefficients of power series for transcendental functions) have been implemented since the very earliest operating systems.^{[citation needed]}

In 1980 Martin Hellman first proposed using a time–memory tradeoff for cryptanalysis.^[1]

Types of tradeoff

Lookup tables vs. recalculation

The most common situation is an algorithm involving a lookup table: an implementation can include the entire table, which reduces computing time, but increases the amount of memory needed, or it can compute table entries as needed, increasing computing time, but reducing memory requirements.

Compressed vs. uncompressed data

A space–time tradeoff can be applied to the problem of data storage. If data is stored uncompressed, it takes more space but less time than if the data were stored compressed (since compressing the data reduces the amount of space it takes, but it takes time to run the decompression algorithm). Depending on the particular instance of the problem, either way is practical. There are also rare instances where it is possible to directly work with compressed data, such as in the case of compressed bitmap indices, where it is faster to work with compression than without compression.

Re-rendering vs. stored images

Storing only the LaTeX source and rendering it as an image every time the page is requested would be trading time for space; more time used, but less space. Rendering the image when the page is changed and storing the rendered images would be trading space for time; more space used, but less time. This technique is more generally known as caching.

Smaller code vs. loop unrolling

Larger code size can be traded for higher program speed when applying loop unrolling. This technique makes the code longer for each iteration of a loop, but saves the computation time required for jumping back to the beginning of the loop at the end of each iteration.

Other examples

Algorithms that also make use of space–time tradeoffs include:

• Baby-step giant-step algorithm for calculating discrete logarithms
• Rainbow tables in cryptography, where the adversary is trying to do better than the exponential time required for a brute-force attack. Rainbow tables use partially precomputed values in the hash space of a cryptographic hash function to crack passwords in minutes instead of weeks. Decreasing the size of the rainbow table increases the time required to iterate over the hash space.
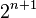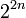• The meet-in-the-middle attack uses a space–time tradeoff to find the cryptographic key in only encryptions (and space) versus the expected encryptions (but only 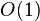space) of the naive attack.
• Dynamic programming, where the time complexity of a problem can be reduced significantly by using more memory.

See also

• Algorithmic efficiency
• Computational resource
• Blum's speedup theorem
• Savitch's theorem

External links

• Philippe Oechslin: Making a Faster Cryptanalytic Time-Memory Trade-Off.
• Once Upon a Time-Memory Tradeoff.

References