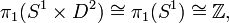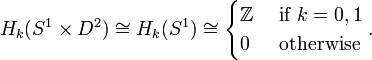Solid torus
From Wikipedia, the free encyclopedia
In mathematics, a solid torus is a topological space homeomorphic to  , i.e. the cartesian product of the circle with a two dimensional disc endowed with the product topology. The solid torus is a connected, compact, orientable 3-dimensional manifold with boundary. The boundary is homeomorphic to
, i.e. the cartesian product of the circle with a two dimensional disc endowed with the product topology. The solid torus is a connected, compact, orientable 3-dimensional manifold with boundary. The boundary is homeomorphic to  , the ordinary torus.
, the ordinary torus.

Solid torus
A standard way to picture a solid torus is as a toroid, embedded in 3-space.
Since the disk 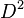 is contractible, the solid torus has the homotopy type of
is contractible, the solid torus has the homotopy type of  . Therefore the fundamental group and homology groups are isomorphic to those of the circle:
. Therefore the fundamental group and homology groups are isomorphic to those of the circle:
See also
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.