Snub polyhedron

A snub polyhedron is a polyhedron obtained by adding extra triangles around each vertex.

Chiral snub polyhedra do not have reflection symmetry and hence have two enantiomorphous forms which are reflections of each other. Their symmetry groups are all point groups and are one of:

• O - chiral octahedral symmetry;the rotation group of the cube and octahedron; order 24.
• I - chiral icosahedral symmetry; the rotation group of the icosahedron and the dodecahedron; order 60.

For example, the snub cube:

Snub polyhedra have Wythoff symbol | p q r and by extension, vertex configuration 3.p.3.q.3.r.

List of snub polyhedra

Uniform

There are 12 uniform snub polyhedra, not including the icosahedron as a snub tetrahedron, the great icosahedron as a retrosnub tetrahedron and the great disnub dirhombidodecahedron, also known as Skilling's figure.

When the Schwarz triangle of the snub polyhedron is isosceles, the snub polyhedron is not chiral.

Snub polyhedron	Image	Original polyhedron	Image	Symmetry group
Icosahedron		Tetrahedron		Ih
Great icosahedron		Octahedron		Ih
Snub cube		Cuboctahedron		O
Snub dodecahedron		Icosidodecahedron		I
Great snub dodecicosidodecahedron		Great dodecicosidodecahedron		I
Snub icosidodecadodecahedron		Icosidodecadodecahedron		I
Snub dodecadodecahedron		Dodecadodecahedron		I
Inverted snub dodecadodecahedron		Dodecadodecahedron		I
Great inverted snub icosidodecahedron		Great icosidodecahedron		I
Great retrosnub icosidodecahedron		Great icosidodecahedron		I
Great snub icosidodecahedron		Great icosidodecahedron		I
Small snub icosicosidodecahedron		Small icosicosidodecahedron		Ih
Small retrosnub icosicosidodecahedron		Small icosicosidodecahedron		Ih
Great dirhombicosidodecahedron				Ih
Great disnub dirhombidodecahedron		Great dirhombicosidodecahedron		Ih

Notes:

• The icosahedron, snub cube and snub dodecahedron are the only three convex ones. They are obtained by snubification of the octahedron, cuboctahedron and the icosidodecahedron - the three convex quasiregular polyhedra.
• The only snub polyhedron with the chiral octahedral group of symmetries is the snub cube.
• Only the icosahedron and the great icosahedron are also regular polyhedra. They are also deltahedra.
• Only the first two and the last four also have reflective symmetries.

There is also the infinite set of antiprisms. They are formed from dihedra, degenerate regular polyhedra. Those up to hexagonal are listed below.

Snub polyhedron	Image	Original polyhedron	Symmetry group
Tetrahedron		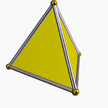Digonal dihedron	Td
Octahedron		Trigonal dihedron	Oh
Square antiprism		Tetragonal dihedron	D4d
Pentagonal antiprism		Pentagonal dihedron	D5d
Pentagrammic antiprism		Pentagrammic dihedron	D5d
Pentagrammic crossed-antiprism		Pentagrammic dihedron	D5d
Hexagonal antiprism		Hexagonal dihedron	D6d

Notes:

• Two of these polyhedra may be constructed from the first two snub polyhedra in the list starting with the icosahedron: the pentagonal antiprism is a parabidiminished icosahedron and a pentagrammic crossed-antiprism is a parabidiminished great icosahedron, also known as a parabireplenished great icosahedron.

Non-uniform

Two Johnson solids are snub polyhedra: the snub disphenoid and the snub square antiprism. Neither is chiral.

Snub polyhedron	Image	Original polyhedron	Image	Symmetry group
Snub disphenoid		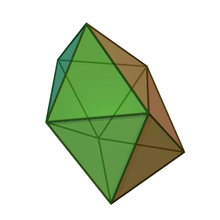Disphenoid		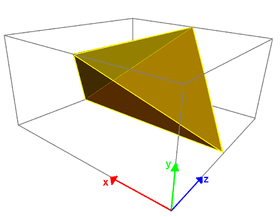D2d
Snub square antiprism		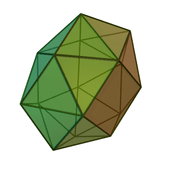Square antiprism		D4d

Notes:

• Only the snub disphenoid is a deltahedron.

References

• Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954), "Uniform polyhedra", Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences 246: 401–450, doi:10.1098/rsta.1954.0003, ISSN 0080-4614, JSTOR 91532, MR 0062446 
• Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9. 
• Skilling, J. (1975), "The complete set of uniform polyhedra", Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences 278: 111–135, doi:10.1098/rsta.1975.0022, ISSN 0080-4614, JSTOR 74475, MR 0365333 
• Mäder, R. E. Uniform Polyhedra. Mathematica J. 3, 48-57, 1993.

Seed	Truncation	Rectification	Bitruncation	Dual	Expansion	Omnitruncation	Snub
t0{p,q} {p,q}	t01{p,q} t{p,q}	t1{p,q} r{p,q}	t12{p,q} 2t{p,q}	t2{p,q} 2r{p,q}	t02{p,q} rr{p,q}	t012{p,q} tr{p,q}	ht012{p,q} sr{p,q}