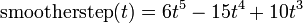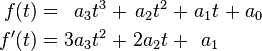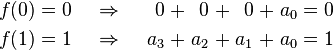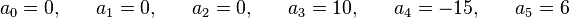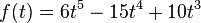Smoothstep

From Wikipedia, the free encyclopedia

A plot of the smoothstep(x) and smootherstep(x) functions.

Smoothstep is a scalar interpolation function commonly used in computer graphics^[1]^[2] and video game engines.^[3] The function interpolates smoothly between two input values based on a third one that should be between the first two. The returned value is clamped between 0 and 1.

The slope of the smoothstep function tends toward zero at both edges. This makes it easy to create a sequence of transitions using smoothstep to interpolate each segment rather than using a more sophisticated or expensive interpolation technique.

As pointed out in MSDN and OpenGL documentation, smoothstep implements cubic Hermite interpolation after doing a clamp:

$\operatorname {smoothstep}(t)=3t^{2}-2t^{3}$

An example implementation provided by AMD^[4] follows.

float smoothstep(float edge0, float edge1, float x)
{
    // Scale, bias and saturate x to 0..1 range
    x = saturate((x - edge0)/(edge1 - edge0)); 
    // Evaluate polynomial
    return x*x*(3 - 2*x);
}

Variations

Ken Perlin suggests^[5] an improved version of the smoothstep function which has zero 1st and 2nd order derivatives at t=0 and t=1:

$\operatorname {smootherstep}(t)=6t^{5}-15t^{4}+10t^{3}$

Reference implementation:

float smootherstep(float edge0, float edge1, float x)
{
    // Scale, and clamp x to 0..1 range
    x = clamp((x - edge0)/(edge1 - edge0), 0.0, 1.0);
    // Evaluate polynomial
    return x*x*x*(x*(x*6 - 15) + 10);
}

Origin

3rd order equation

We start with a generic third order polynomial function and its first derivative:

${\begin{alignedat}{9}f(t)&&\;=\;&&a_{3}t^{3}&&\;+\;&&a_{2}t^{2}&&\;+\;&&a_{1}t&&\;+\;&&a_{0}&\\f'(t)&&\;=\;&&3a_{3}t^{2}&&\;+\;&&2a_{2}t&&\;+\;&&a_{1}&\end{alignedat}}$

Applying the desired values for the function at both endpoints we get:

${\begin{alignedat}{13}f(0)&&\;=\;&&0\;\;\;\;\;&&\Rightarrow &&\;\;\;\;\;0\;&&+&&\;0\;&&+&&\;0\;&&+&&\;a_{0}&&\;=\;&&0&\\f(1)&&\;=\;&&1\;\;\;\;\;&&\Rightarrow &&\;\;\;\;\;a_{3}\;&&+&&\;a_{2}\;&&+&&\;a_{1}\;&&+&&\;a_{0}&&\;=\;&&1&\end{alignedat}}$

Applying the desired values for the first derivative of the function at both endpoints we get:

${\begin{alignedat}{11}f'(0)&&\;=\;&&0\;\;\;\;&&\Rightarrow &&\;\;\;\;0\;&&+&&\;0\;&&+&&\;a_{1}\;&&=\;&&0&\\f'(1)&&\;=\;&&0\;\;\;\;&&\Rightarrow &&\;\;\;\;3a_{3}\;&&+&&\;2a_{2}\;&&+&&\;a_{1}\;&&=\;&&0&\end{alignedat}}$

Solving the system of 4 unknowns formed by the last 4 equations we obtain the values of the polynomial coefficients:

$a_{0}=0,\;\;\;\;\;\;a_{1}=0,\;\;\;\;\;\;a_{2}=3,\;\;\;\;\;\;a_{3}=-2$

Introducing these coefficients back into the first equation gives the third order smoothstep function:

$f(t)=-2t^{3}+3t^{2}$

5th order equation

We start with a generic fifth order polynomial function, its first derivative and its second derivative:

${\begin{alignedat}{13}f(t)&&\;=\;&&a_{5}t^{5}&&\;+\;&&a_{4}t^{4}&&\;+\;&&a_{3}t^{3}&&\;+\;&&a_{2}t^{2}&&\;+\;&&a_{1}t&&\;+\;&&a_{0}&\\f'(t)&&\;=\;&&5a_{5}t^{4}&&\;+\;&&4a_{4}t^{3}&&\;+\;&&3a_{3}t^{2}&&\;+\;&&2a_{2}t&&\;+\;&&a_{1}&\\f''(t)&&\;=\;&&20a_{5}t^{3}&&\;+\;&&12a_{4}t^{2}&&\;+\;&&6a_{3}t&&\;+\;&&2a_{2}&\end{alignedat}}$

Applying the desired values for the function at both endpoints we get:

${\begin{alignedat}{17}f(0)&&\;=\;&&0\;\;\;\;\;&&\Rightarrow &&\;\;\;\;\;0\;&&+&&\;0\;&&+&&\;0\;&&+&&\;0\;&&+&&\;0\;&&+&&\;a_{0}&&\;=\;&&0&\\f(1)&&\;=\;&&1\;\;\;\;\;&&\Rightarrow &&\;\;\;\;\;a_{5}\;&&+&&\;a_{4}\;&&+&&\;a_{3}\;&&+&&\;a_{2}\;&&+&&\;a_{1}\;&&+&&\;a_{0}&&\;=\;&&1&\end{alignedat}}$

Applying the desired values for the first derivative of the function at both endpoints we get:

${\begin{alignedat}{15}f'(0)&&\;=\;&&0\;\;\;\;&&\Rightarrow &&\;\;\;\;0\;&&+&&\;0\;&&+&&\;0\;&&+&&\;0\;&&+&&\;a_{1}\;&&=\;&&0&\\f'(1)&&\;=\;&&0\;\;\;\;&&\Rightarrow &&\;\;\;\;5a_{5}\;&&+&&\;4a_{4}\;&&+&&\;3a_{3}\;&&+&&\;2a_{2}\;&&+&&\;a_{1}\;&&=\;&&0&\end{alignedat}}$

Applying the desired values for the second derivative of the function at both endpoints we get:

${\begin{alignedat}{15}f''(0)&&\;=\;&&0\;\;\;\;&&\Rightarrow &&\;\;\;\;0\;&&+&&\;0\;&&+&&\;0\;&&+&&\;2a_{2}\;&&=\;&&0&\\f''(1)&&\;=\;&&0\;\;\;\;&&\Rightarrow &&\;\;\;\;20a_{5}\;&&+&&\;12a_{4}\;&&+&&\;6a_{3}\;&&+&&\;2a_{2}\;&&=\;&&0&\end{alignedat}}$

Solving the system of 6 unknowns formed by the last 6 equations we obtain the values of the polynomial coefficients:

$a_{0}=0,\;\;\;\;\;\;a_{1}=0,\;\;\;\;\;\;a_{2}=0,\;\;\;\;\;\;a_{3}=10,\;\;\;\;\;\;a_{4}=-15,\;\;\;\;\;\;a_{5}=6$

Introducing these coefficients back into the first equation gives the fifth order smoothstep function:

$f(t)=6t^{5}-15t^{4}+10t^{3}$

References

External links

Using smoothstep (in the RenderMan Shading Language) by Prof. Malcolm Kesson.
Interpolation tricks by Jari Komppa

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.