Smooth scheme

From Wikipedia, the free encyclopedia

In algebraic geometry, a smooth scheme X of dimension n over an algebraically closed field k is an algebraic scheme^[1] that is regular and has dimension n. More generally, an algebraic scheme over a field k is said to be smooth if 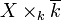$X\times _{k}\overline {k}$ is smooth for any algebraic closure 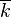$\overline {k}$ of k.

If k is perfect, then an algebraic scheme over k is smooth if and only if it is regular.

There is also a notion of a "smooth morphism" between schemes, and the above definition coincides with it. That is, an algebraic scheme X over k is smooth of dimension n if and only if 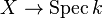$X\to \operatorname {Spec}k$ is smooth of relative dimension n.

Properties

A smooth scheme is connected if and only if it is irreducible. A connected smooth scheme is normal.^{[citation needed]}

Generic smoothness

A scheme X is said to be generically smooth of dimension n over k if X contains an open dense subset that is smooth of dimension n over k. Any integral scheme over a perfect field (in particular an algebraically closed field) is generically smooth.

Examples

Examples of smooth schemes are:

A nonsingular variety.
A linear algebraic group.

Notes

↑ By "algebraic scheme" we mean a scheme of finite type over a field.

References

D. Gaitsgory's notes on flatness and smoothness at http://www.math.harvard.edu/~gaitsgde/Schemes_2009/BR/SmoothMaps.pdf
Hartshorne, Robin (1977), Algebraic Geometry, Graduate Texts in Mathematics 52, New York: Springer-Verlag, ISBN 978-0-387-90244-9, MR 0463157