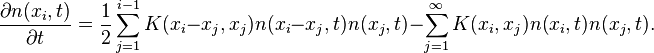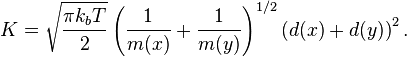Smoluchowski coagulation equation

From Wikipedia, the free encyclopedia

In statistical physics, the Smoluchowski coagulation equation is an integrodifferential equation introduced by Marian Smoluchowski in a seminal 1916 publication,[1] describing the time evolution of the number density of particles as they coagulate (in this context "clumping together") to size x at time t.

Equation

In the case when the sizes of the coagulated particles are continuous variables, the equation involves an integral:

{\frac {\partial n(x,t)}{\partial t}}={\frac {1}{2}}\int _{0}^{x}K(x-y,y)n(x-y,t)n(y,t)\,dy-\int _{0}^{\infty }K(x,y)n(x,t)n(y,t)\,dy.

If dy is interpreted as a discrete measure, i.e. when particles join in discrete sizes, then the discrete form of the equation is a summation:

{\frac {\partial n(x_{i},t)}{\partial t}}={\frac {1}{2}}\sum _{{j=1}}^{{i-1}}K(x_{i}-x_{j},x_{j})n(x_{i}-x_{j},t)n(x_{j},t)-\sum _{{j=1}}^{\infty }K(x_{i},x_{j})n(x_{i},t)n(x_{j},t).

Coagulation kernel

The operator, K, is known as the coagulation kernel and describes the rate at which particles of size x coagulate with particles of size y. Analytic solutions to the equation exist when the kernel takes one of three simple forms:

K=1,\quad K=x+y,\quad K=xy,

known as the constant, additive, and multiplicative kernels respectively. However, in most practical applications the kernel takes on a significantly more complex form, for example the free-molecular kernel which describes collisions in a dilute gas-phase system,

K={\sqrt {{\frac {\pi k_{b}T}{2}}}}\left({\frac {1}{m(x)}}+{\frac {1}{m(y)}}\right)^{{1/2}}\left(d(x)+d(y)\right)^{2}.

Generally the coagulation equations that result from such physically realistic kernels are not solvable, and as such, it is necessary to appeal to numerical methods. There exist well-established deterministic methods that can be used when there is only one particle property (x) of interest, the two principal ones being the method of moments and sectional methods. In the multi-variate case however, when two or more properties (such as size, shape, composition etc.) are introduced, special approximation methods that suffer less from curse of dimensionality has to be applied. For instance, approximation based on Gaussian radial basis functions has been successfully applied to the two-dimensional coagulation equation.[2]

When accuracy of the solution is not of primary importance, stochastic particle (Monte-Carlo) methods are an attractive alternative.

See also

References

  1. ↑ Smoluchowski, Marian (1916). "Drei Vorträge über Diffusion, Brownsche Molekularbewegung und Koagulation von Kolloidteilchen". Physik. Z. 17: 557–571, 585–599. Bibcode:1916ZPhy...17..557S. 
  2. ↑ Predicting multidimensional distributive properties of hyperbranched polymer resulting from AB2 polymerization with substitution, cyclization and shielding, I. Kryven, P.D. Iedema, Polymer 54 (14), 3472–3484
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.