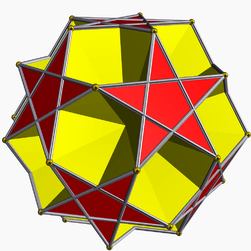
Small dodecahemicosahedron
| Small dodecahemicosahedron | |
|---|---|
 | |
| Type | Uniform star polyhedron |
| Elements | F = 22, E = 60 V = 30 (χ = −8) |
| Faces by sides | 12{5/2}+10{6} |
| Wythoff symbol(s) | 5/3 5/2 | 3 (double covering) |
| Symmetry group | Ih, [5,3], *532 |
| Index references | U62, C78, W100 |
| Bowers acronym | Sidhei |
 6.5/2.6.5/3 (Vertex figure) |
 Small dodecahemicosacron (dual polyhedron) |
In geometry, the small dodecahemicosahedron is a nonconvex uniform polyhedron, indexed as U62. Its vertex figure is a crossed quadrilateral.
It is a hemipolyhedron with ten hexagonal faces passing through the model center.
Related polyhedra
Its convex hull is the icosidodecahedron. It also shares its edge arrangement with the dodecadodecahedron (having the pentagrammic faces in common), and with the great dodecahemicosahedron (having the hexagonal faces in common).
 Dodecadodecahedron |
 Small dodecahemicosahedron |
 Great dodecahemicosahedron |
 Icosidodecahedron (convex hull) |
Filling
There is some controversy on how to colour the faces of this polyhedron. Although the common way to fill in a polygon is to just colour its whole interior, the middle of the pentagrams are over empty space, as can be seen from the picture of the great dodecahemicosahedron above. Hence, some, such as Jonathan Bowers, do not fill in the middle of the pentagram: this filling has been called "neo filling". In the neo filling, orientable polyhedra are filled traditionally, but non-orientable polyhedra have their faces filled with the modulo-2 method (only odd-density regions are filled in).[1]
 Traditional filling |
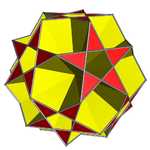 "Neo filling" |