Small-gain theorem

From Wikipedia, the free encyclopedia

In nonlinear systems, the formalism of input-output stability is an important tool in studying the stability of interconnected systems since the gain of a system directly relates to how the norm of a signal increases or decreases as it passes through the system. The small-gain theorem gives a sufficient condition for finite-gain {\mathcal {L}} stability of the feedback connection. The small gain theorem was proved by George Zames in 1966. It can be seen as a generalization of the Nyquist criterion to non-linear time varying MIMO systems (systems with multiple inputs and multiple outputs).

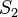Theorem. Assume two stable systems S_{1} and S_{2} are connected in a feedback loop, then the closed loop system is input-output stable if 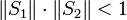\|S_{1}\|\cdot \|S_{2}\|<1. (The norm can be the infinity norm, that is the size of the largest singular value of the transfer function over all frequencies. Also any induced Norm will lead to the same results).[1][2]

Notes

  1. ↑ Glad, Ljung: Control Theory, Page 19
  2. ↑ Glad, Ljung: Control Theory (Edition 2:6), Page 31

References

  • H. K. Khalil, Nonlinear Systems, third edition, Prentice Hall, Upper Saddle River, New Jersey, 2002;
  • C. A. Desoer, M. Vidyasagar, Feedback Systems: Input-Output Properties, second edition, SIAM, 2009.


This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.