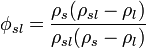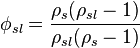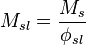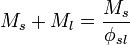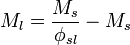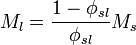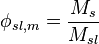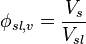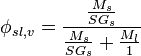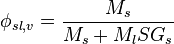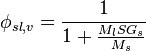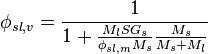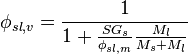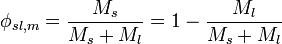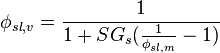Slurry

From Wikipedia, the free encyclopedia

For the settlement in the North West province of South Africa, see Slurry, North West.

A slurry composed of glass beads in silicone oil flowing down an inclined plane.

A slurry is a thin sloppy mud or cement or, in extended use, any fluid mixture of a pulverized solid with a liquid (usually water), often used as a convenient way of handling solids in bulk.^[1] Slurries behave in some ways like thick fluids, flowing under gravity but are also capable of being pumped if not too thick.

Examples

Examples of slurries include:

Cement slurry, a mixture of cement, water, and assorted dry and liquid additives used in the petroleum and other industries^[2]^[3]
Soil/cement slurry, also called Controlled Low-Strength Material (CLSM), flowable fill, controlled density fill, flowable mortar, plastic soil-cement, K-Krete, and other names^[4]
A mixture of thickening agent, oxidizers, and water used to form a gel explosive^{[citation needed]}
A mixture of pyroclastic material, rocky debris, and water produced in a volcanic eruption and known as a lahar
A mixture of bentonite and water used to make slurry walls
Coal slurry, a mixture of coal waste and water, or crushed coal and water^[5]
A mixture of wood pulp and water used to make paper
A mixture of animal waste, organic matter, and sometimes water known simply as "slurry" in agricultural use, used as fertilizer after ageing in a slurry pit
Meat slurry, a mixture of finely ground meat and water, centrifugally dewatered and used as food
An abrasive substance used in chemical-mechanical polishing
Slurry ice, a mixture of ice crystals, freezing point depressant, and water
A mixture of raw materials and water involved in the rawmill manufacture of Portland cement
A mixture of minerals, water, and additives used in the manufacture of ceramics
A bolus of chewed food mixed with saliva^[6]

Calculations

Determining solids fraction

To determine the percent solids (or solids fraction) of a slurry from the density of the slurry, solids and liquid^[7]

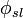$\phi _{{sl}}={\frac {\rho _{{s}}(\rho _{{sl}}-\rho _{{l}})}{\rho _{{sl}}(\rho _{{s}}-\rho _{{l}})}}$

where

$\phi _{{sl}}$ is the solids fraction of the slurry (state by volume)

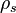$\rho _{{s}}$ is the solids density

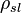$\rho _{{sl}}$ is the slurry density

$\rho _{{l}}$ is the liquid density

In aqueous slurries, as is common in mineral processing, the specific gravity of the species is typically used, and since $SG_{{water}}$ is taken to be 1, this relation is typically written:

$\phi _{{sl}}={\frac {\rho _{{s}}(\rho _{{sl}}-1)}{\rho _{{sl}}(\rho _{{s}}-1)}}$

even though specific gravity with units tons/m^3 is used instead of the SI density unit, kg/m^3.

Liquid mass from mass fraction of solids

To determine the mass of liquid in a sample given the mass of solids and the mass fraction: By definition

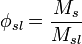$\phi _{{sl}}={\frac {M_{{s}}}{M_{{sl}}}}$ *100

therefore

$M_{{sl}}={\frac {M_{{s}}}{\phi _{{sl}}}}$

and

$M_{{s}}+M_{{l}}={\frac {M_{{s}}}{\phi _{{sl}}}}$

then

$M_{{l}}={\frac {M_{{s}}}{\phi _{{sl}}}}-M_{{s}}$

and therefore

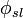$M_{{l}}={\frac {1-\phi _{{sl}}}{\phi _{{sl}}}}M_{{s}}$

where

$\phi _{{sl}}$ is the solids fraction of the slurry

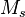$M_{{s}}$ is the mass or mass flow of solids in the sample or stream

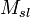$M_{{sl}}$ is the mass or mass flow of slurry in the sample or stream

$M_{{l}}$ is the mass or mass flow of liquid in the sample or stream

Volumetric fraction from mass fraction

$\phi _{{sl,m}}={\frac {M_{{s}}}{M_{{sl}}}}$

Equivalently

$\phi _{{sl,v}}={\frac {V_{{s}}}{V_{{sl}}}}$

and in a minerals processing context where the specific gravity of the liquid (water) is taken to be one:

$\phi _{{sl,v}}={\frac {{\frac {M_{{s}}}{SG_{{s}}}}}{{\frac {M_{{s}}}{SG_{{s}}}}+{\frac {M_{{l}}}{1}}}}$

$\phi _{{sl,v}}={\frac {M_{{s}}}{M_{{s}}+M_{{l}}SG_{{s}}}}$

and

$\phi _{{sl,v}}={\frac {1}{1+{\frac {M_{{l}}SG_{{s}}}{M_{{s}}}}}}$

Then combining with the first equation:

$\phi _{{sl,v}}={\frac {1}{1+{\frac {M_{{l}}SG_{{s}}}{\phi _{{sl,m}}M_{{s}}}}{\frac {M_{{s}}}{M_{{s}}+M_{{l}}}}}}$

$\phi _{{sl,v}}={\frac {1}{1+{\frac {SG_{{s}}}{\phi _{{sl,m}}}}{\frac {M_{{l}}}{M_{{s}}+M_{{l}}}}}}$

Then since

$\phi _{{sl,m}}={\frac {M_{{s}}}{M_{{s}}+M_{{l}}}}=1-{\frac {M_{{l}}}{M_{{s}}+M_{{l}}}}$

we conclude that

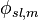$\phi _{{sl,v}}={\frac {1}{1+SG_{{s}}({\frac {1}{\phi _{{sl,m}}}}-1)}}$

where

$\phi _{{sl,v}}$ is the solids fraction of the slurry on a volumetric basis

$\phi _{{sl,m}}$ is the solids fraction of the slurry on a mass basis

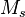$M_{{s}}$ is the mass or mass flow of solids in the sample or stream

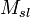$M_{{sl}}$ is the mass or mass flow of slurry in the sample or stream

$M_{{l}}$ is the mass or mass flow of liquid in the sample or stream

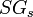$SG_{{s}}$ is the bulk specific gravity of the solids

References

↑ Oxford English Dictionary 2nd ed.: Slurry
↑ Shlumberger: Oilfield glossary
↑ Rheonova : Measuring rheological propertis of settling slurries
↑ Portland Cement Association: Controlled Low-Strength Material
↑ Red Valve Company: Coal Slurry Pipeline
↑ Rheonova : Measuring food bolus properties
↑ Wills, B.A. and Napier-Munn, T.J, Wills' Mineral Processing Technology: an introduction to the practical aspects of ore treatment and mineral recovery, ISBN 978-0-7506-4450-1, Seventh Edition (2006), Elsevier, Great Britain

External links

Look up slurry in Wiktionary, the free dictionary.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.

Slurry

Examples

Calculations

Determining solids fraction

Liquid mass from mass fraction of solids

Volumetric fraction from mass fraction

See also

References

External links