Slide attack

From Wikipedia, the free encyclopedia

The slide attack is a form of cryptanalysis designed to deal with the prevailing idea that even weak ciphers can become very strong by increasing the number of rounds, which can ward off a differential attack. The slide attack works in such a way as to make the number of rounds in a cipher irrelevant. Rather than looking at the data-randomizing aspects of the block cipher, the slide attack works by analyzing the key schedule and exploiting weaknesses in it to break the cipher. The most common one is the keys repeating in a cyclic manner.

The attack was first described by David Wagner and Alex Biryukov. Bruce Schneier first suggested the term slide attack to them, and they used it in their 1999 paper describing the attack.

The only requirements for a slide attack to work on a cipher is that it can be broken down into multiple rounds of an identical F function. This probably means that it has a cyclic key schedule. The F function must be vulnerable to a known-plaintext attack. The slide attack is closely related to the related-key attack.

The idea of the slide attack has roots in a paper published by Edna Grossman and Bryant Tuckerman in an IBM Technical Report in 1977. Grossman and Tuckerman demonstrated the attack on a weak block cipher named New Data Seal (NDS). The attack relied on the fact that the cipher has identical subkeys in each round, so the cipher had a cyclic key schedule with a cycle of only one key, which makes it an early version of the slide attack. A summary of the report, including a description of the NDS block cipher and the attack, is given in Cipher Systems (Beker & Piper, 1982).

The actual attack

First, to introduce some notation. In this section assume the cipher takes n bit blocks and has a key-schedule using $K_{1}\cdots K_{m}$ as keys of any length.

The slide attack works by breaking the cipher up into identical permutation functions, F. This F function may consist of more than one round of the cipher; it is defined by the key-schedule. For example, if a cipher uses an alternating key schedule where it switches between a $K_{1}$ and $K_{2}$ for each round, the F function would consist of two rounds. Each of the $K_{i}$ will appear at least once in F.

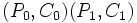The next step is to collect $2^{{n/2}}$ plaintext-ciphertext pairs. Depending on the characteristics of the cipher fewer may suffice, but by the birthday paradox no more than $2^{{n/2}}$ should be needed. These pairs, which denoted as $(P,C)$ are then used to find a slid pair which is denoted $(P_{0},C_{0})(P_{1},C_{1})$ . A slid pair has the property that $P_{0}=F(P_{1})$ and that $C_{0}=F(C_{1})$ . Once a slid pair is identified, the cipher is broken because of the vulnerability to known-plaintext attacks. The key can easily be extracted from this pairing. The slid pair can be thought to be what happens to a message after one application of the function F. It is ’slid’ over one encryption round and this is where the attack gets its name.

The process of finding a slid pair is somewhat different for each cipher but follows the same basic scheme. One uses the fact that it is relatively easy to extract the key from just one iteration of F. Choose any pair of plaintext-ciphertext pairs, 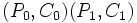$(P_{0},C_{0})(P_{1},C_{1})$ and check to see what the keys corresponding to $P_{0}=F(P_{1})$ and $C_{0}=F(C_{1})$ are. If these keys match, this is a slid pair; otherwise move on to the next pair.

With $2^{{n/2}}$ plaintext-ciphertext pairs one slid pair is expected, along with a small number of false-positives depending on the structure of the cipher. The false positives can be eliminated by using the keys on a different message-ciphertext pair to see if the encryption is correct. The probability that the wrong key will correctly encipher two or more messages is very low for a good cipher.

Sometimes the structure of the cipher greatly reduces the number of plaintext-ciphertext pairs needed, and thus also a large amount of the work. The clearest of these examples is the Feistel cipher using a cyclic key schedule. The reason for this is given a 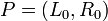$P=(L_{0},R_{0})$ the search is for a 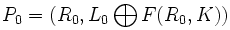$P_{0}=(R_{0},L_{0}\bigoplus F(R_{0},K))$ . 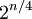This reduces the possible paired messages from $2^{n}$ down to $2^{{n/2}}$ (since half the message is fixed) and so at most $2^{{n/4}}$ plaintext-ciphertext pairs are needed in order to find a slid-pair.

References

E.K. Grossman and B. Tuckerman (1977). Analysis of a Feistel-like cipher weakened by having no rotating key. IBM Thomas J. Watson Research Report RC 6375.
Henry Beker and Fred Piper (1982). Cipher Systems: The Protection of Communications. John Wiley & Sons. pp. 263–267. ISBN 0-471-89192-4. (contains a summary of the paper by Grossman and Tuckerman)
Alex Biryukov and David Wagner (March 1999). "Slide Attacks" (PDF/PostScript). 6th International Workshop on Fast Software Encryption (FSE '99). Rome: Springer-Verlag. pp. pp.245–259. Retrieved 2007-09-03.
Alex Biryukov and David Wagner (May 2000). "Advanced Slide Attacks" (PDF/PostScript). Advances in Cryptology, Proceedings of EUROCRYPT 2000. Bruges: Springer-Verlag. pp. pp.589–606. Retrieved 2007-09-03.
S. Furuya (December 2001). "Slide Attacks with a Known-Plaintext Cryptanalysis" (PDF). 4th International Conference on Information Security and Cryptology (ICISC 2001). Seoul: Springer-Verlag. pp. pp.214–225. Retrieved 2007-09-03.
Eli Biham (1994). "New Types of Cryptanalytic Attacks Using Related Keys" (PDF/PostScript). Journal of Cryptology 7 (4): pp.229–246. ISSN 0933-2790. Retrieved 2007-09-03.
M. Ciet, G. Piret, J. Quisquater (2002). Related-Key and Slide Attacks: Analysis, Connections, and Improvements (PDF/PostScript). Retrieved 2007-09-04.

v t e Block ciphers (security summary)

Common algorithms	AES Blowfish DES Triple DES Serpent Twofish

Less common algorithms	Camellia CAST-128 IDEA RC2 RC5 SEED Skipjack TEA XTEA

Other algorithms	3-Way Akelarre Anubis ARIA BaseKing BassOmatic BATON BEAR and LION CAST-256 Chiasmus CIKS-1 CIPHERUNICORN-A CIPHERUNICORN-E CLEFIA CMEA Cobra COCONUT98 Crab Cryptomeria/C2 CRYPTON CS-Cipher DEAL DES-X DFC E2 FEAL FEA-M FROG G-DES GOST Grand Cru Hasty Pudding cipher Hierocrypt ICE IDEA NXT Intel Cascade Cipher Iraqi KASUMI KeeLoq KHAZAD Khufu and Khafre KN-Cipher Ladder-DES Libelle LOKI97 LOKI89/91 Lucifer M6 M8 MacGuffin Madryga MAGENTA MARS Mercy MESH MISTY1 MMB MULTI2 MultiSwap New Data Seal NewDES Nimbus NOEKEON NUSH PRESENT Q RC6 REDOC Red Pike S-1 SAFER SAVILLE SC2000 SHACAL SHARK Simon SMS4 Speck Spectr-H64 Square SXAL/MBAL Threefish Treyfer UES Xenon xmx XXTEA Zodiac

Design	Feistel network Key schedule Lai-Massey scheme Product cipher S-box P-box SPN Avalanche effect Block size Key size Key whitening No weak keys

Attack (cryptanalysis)	Brute-force (EFF DES cracker) MITM Linear (Piling-up lemma) Differential (Impossible Truncated Higher-order) Differential-linear Integral (aka Square) Boomerang Mod n Related-key Slide Rotational Timing XSL Interpolation Partitioning Davies' Rebound

Standardization	AES process CRYPTREC NESSIE

Utilization	Initialization vector Mode of operation Padding

v t e Cryptography

History of cryptography Cryptanalysis Cryptography portal Outline of cryptography

Symmetric-key algorithm Block cipher Stream cipher Public-key cryptography Cryptographic hash function Message authentication code Random numbers Steganography

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.