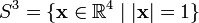Slice knot

From Wikipedia, the free encyclopedia

A slice knot is a type of mathematical knot. It helps to remember that in knot theory, a "knot" means an embedded circle in the 3-sphere

S^{3}=\{{\mathbf {x}}\in {\mathbb {R}}^{4}\mid |{\mathbf {x}}|=1\}

and that the 3-sphere can be thought of as the boundary of the four-dimensional ball

B^{4}=\{{\mathbf {x}}\in {\mathbb {R}}^{4}\mid |{\mathbf {x}}|\leq 1\}.

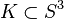A knot K\subset S^{3} is slice if it bounds a nicely embedded disk D in the 4-ball.

What is meant by "nicely embedded" depends on the context, and there are different terms for different kinds of slice knots. If D is smoothly embedded in B4, then K is said to be smoothly slice. If K is only locally flat (which is weaker), then K is said to be topologically slice.

Any ribbon knot is smoothly slice. An old question of Fox asks whether every slice knot is actually a ribbon knot.

The signature of a slice knot is zero.

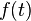The Alexander polynomial of a slice knot factors as a product f(t)f(t^{{-1}}) where f(t) is some integral Laurent polynomial. This is known as the Fox–Milnor condition.

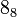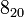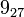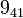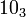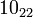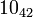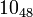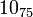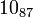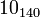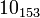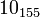The following is a list of all slice knots with 10 or fewer crossings; it was compiled using the Knot Atlas: 61, 8_{8}, 8_{9}, 8_{{20}}, 9_{{27}}, 9_{{41}}, 9_{{46}}, 10_{3}, 10_{{22}}, 10_{{35}}, 10_{{42}}, 10_{{48}}, 10_{{75}}, 10_{{87}}, 10_{{99}}, 10_{{123}}, 10_{{129}}, 10_{{137}}, 10_{{140}}, 10_{{153}} and 10_{{155}}.

See also


This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.