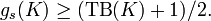Slice genus

In mathematics, the slice genus of a smooth knot K in S³ (sometimes called its Murasugi genus or 4-ball genus) is the least integer <var>g</var> such that K is the boundary of a connected, orientable 2-manifold S of genus g embedded in the 4-ball D⁴ bounded by S³.

More precisely, if S is required to be smoothly embedded, then this integer g is the smooth slice genus of K and is often denoted <var>g_s</var>(K) or <var>g</var>₄(K), whereas if S is required only to be topologically locally flatly embedded then g is the topologically locally flat slice genus of K. (There is no point considering g if S is required only to be a topological embedding, since the cone on K is a 2-disk with genus 0.) There can be an arbitrarily great difference between the smooth and the topologically locally flat slice genus of a knot; a theorem of Michael Freedman says that if the Alexander polynomial of K is 1, then the topologically locally flat slice genus of K is 0, but it can be proved in many ways (originally with gauge theory) that for every <var>g</var> there exist knots K such that the Alexander polynomial of K is 1 while the genus and the smooth slice genus of K both equal <var>g</var>.

The (smooth) slice genus of a knot K is bounded below by a quantity involving the Thurston–Bennequin invariant of K:

The (smooth) slice genus is zero if and only if the knot is concordant to the unknot.

See also

• Slice knot

Further reading

• Rudolph, Lee (1997). "The slice genus and the Thurston-Bennequin invariant of a knot". Proceedings of the American Mathematical Society 125 (10): 3049 3050. doi:10.1090/S0002-9939-97-04258-5. MR 1443854. 

• Livingston, Charles, A survey of classical knot concordance, in: Handbook of knot theory, pp 319–347, Elsevier, Amsterdam, 2005. MR 2179265 ISBN 0-444-51452-X