Skew-Hermitian

From Wikipedia, the free encyclopedia

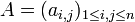An $n$ by $n$ complex or real matrix $A=(a_{{i,j}})_{{1\leq i,j\leq n}}$ is said to be anti-Hermitian, skew-Hermitian, or said to represent a skew-adjoint operator, or to be a skew-adjoint matrix, on the complex or real $n$ dimensional space $K^{n}$ , if its adjoint is the negative of itself: : $A^{*}=-A$ .

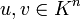Note that the adjoint of an operator depends on the scalar product considered on the $n$ dimensional complex or real space $K^{n}$ . If $(\cdot |\cdot )$ denotes the scalar product on $K^{n}$ , then saying $A$ is skew-adjoint means that for all $u,v\in K^{n}$ one has $(Au|v)=-(u|Av)\,.$

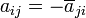In the particular case of the canonical scalar products on $K^{n}$ , the matrix of a skew-adjoint operator satisfies $a_{{ij}}=-{\overline a}_{{ji}}$ for all $1\leq i,j\leq n$ .

Imaginary numbers can be thought of as skew-adjoint (since they are like 1-by-1 matrices), whereas real numbers correspond to self-adjoint operators.

Skew-Hermitian

See also