Skew-Hamiltonian matrix

From Wikipedia, the free encyclopedia

In linear algebra, skew-Hamiltonian matrices are special matrices which correspond to skew-symmetric bilinear forms on a symplectic vector space.

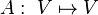Let V be a vector space, equipped with a symplectic form $\Omega$ . Such a space must be even-dimensional. A linear map $A:\;V\mapsto V$ is called a skew-Hamiltonian operator with respect to $\Omega$ if the form $x,y\mapsto \Omega (A(x),y)$ is skew-symmetric.

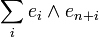Choose a basis $e_{1},...e_{{2n}}$ in V, such that $\Omega$ is written as $\sum _{i}e_{i}\wedge e_{{n+i}}$ . Then a linear operator is skew-Hamiltonian with respect to $\Omega$ if and only if its matrix A satisfies $A^{T}J=JA$ , where J is the skew-symmetric matrix

$J={\begin{bmatrix}0&I_{n}\\-I_{n}&0\\\end{bmatrix}}$

and I_n is the 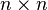$n\times n$ identity matrix.^[1] Such matrices are called skew-Hamiltonian.

The square of a Hamiltonian matrix is skew-Hamiltonian. The converse is also true: every skew-Hamiltonian matrix can be obtained as the square of a Hamiltonian matrix.^[1]^[2]

Notes

↑ 1.0 1.1 William C. Waterhouse, The structure of alternating-Hamiltonian matrices, Linear Algebra and its Applications, Volume 396, 1 February 2005, Pages 385-390
↑ Heike Faßbender, D. Steven Mackey, Niloufer Mackey and Hongguo Xu Hamiltonian Square Roots of Skew-Hamiltonian Matrices, Linear Algebra and its Applications 287, pp. 125 - 159, 1999

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.