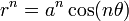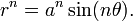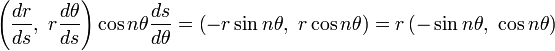Sinusoidal spiral

From Wikipedia, the free encyclopedia

Sinusoidal spirals: equilateral hyperbola (n = -2), line (n = -1), parabola (n = -1/2), cardioid (n = 1/2), circle (n = 1) and lemniscate of Bernoulli (n = 2), where rⁿ = 1ⁿ cos(nθ) in polar coordinates and their equivalents in rectangular coordinates.

In geometry, the sinusoidal spirals are a family of curves defined by the equation in polar coordinates

$r^{n}=a^{n}\cos(n\theta )\,$

where a is a nonzero constant and n is a rational number other than 0. With a rotation about the origin, this can also be written

$r^{n}=a^{n}\sin(n\theta ).\,$

The term "spiral" is a misnomer, because they are not actually spirals, and often have a flower-like shape. Many well known curves are sinusoidal spirals including:

Line (n = −1)
Circle (n = 1)
Equilateral hyperbola (n = −2)
Parabola (n = −1/2)
Cardioid (n = 1/2)
Lemniscate of Bernoulli (n = 2)
Tschirnhausen cubic (n = −1/3)

The curves were first studied by Colin Maclaurin.

Equations

Differentiating

$r^{n}=a^{n}\cos(n\theta )\,$

and eliminating a produces a differential equation for r and θ:

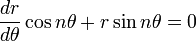${\frac {dr}{d\theta }}\cos n\theta +r\sin n\theta =0$ .

Then

$\left({\frac {dr}{ds}},\ r{\frac {d\theta }{ds}}\right)\cos n\theta {\frac {ds}{d\theta }}=\left(-r\sin n\theta ,\ r\cos n\theta \right)=r\left(-\sin n\theta ,\ \cos n\theta \right)$

which implies that the polar tangential angle is

$\psi =n\theta \pm \pi /2$

and so the tangential angle is

$\varphi =(n+1)\theta \pm \pi /2$ .

(The sign here is positive if r and cos nθ have the same sign and negative otherwise.)

The unit tangent vector,

$\left({\frac {dr}{ds}},\ r{\frac {d\theta }{ds}}\right)$ ,

has length one, so comparing the magnitude of the vectors on each side of the above equation gives

${\frac {ds}{d\theta }}=r\cos ^{{-1}}n\theta =a\cos ^{{-1+{\tfrac {1}{n}}}}n\theta$ .

In particular, the length of a single loop when 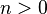$n>0$ is:

$a\int _{{-{\tfrac {\pi }{2n}}}}^{{{\tfrac {\pi }{2n}}}}\cos ^{{-1+{\tfrac {1}{n}}}}n\theta \ d\theta$

The curvature is given by

${\frac {d\varphi }{ds}}=(n+1){\frac {d\theta }{ds}}={\frac {n+1}{a}}\cos ^{{1-{\tfrac {1}{n}}}}n\theta$ .

Properties

The inverse of a sinusoidal spiral with respect to a circle with center at the origin is another sinusoidal spiral whose value of n is the negative of the original curve's value of n. For example, the inverse of the lemniscate of Bernoulli is a hyperbola.

The isoptic, pedal and negative pedal of a sinusoidal spiral are different sinusoidal spirals.

One path of a particle moving according to a central force proportional to a power of r is a sinusoidal spiral.

When n is an integer, and n points are arranged regularly on a circle of radius a, then the set of points so that the geometric mean of the distances from the point to the n points is a sinusoidal spiral. In this case the sinusoidal spiral is a polynomial lemniscate

Wikimedia Commons has media related to Sinusoidal spiral.

References

Yates, R. C.: A Handbook on Curves and Their Properties, J. W. Edwards (1952), "Spiral" p. 213–214
"Sinusoidal spiral" at www.2dcurves.com
"Sinusoidal Spirals" at The MacTutor History of Mathematics
"Spirale Sinusoïdale" at Encyclopédie des Formes Mathématiques Remarquables
Weisstein, Eric W., "Sinusoidal Spiral", MathWorld.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.