Singularity spectrum

From Wikipedia, the free encyclopedia

The singularity spectrum is a function used in Multifractal analysis to describe the fractal dimension of a subset of points of a function belonging to a group of points that have the same Holder exponent. Intuitively, the singularity spectrum gives a value for how "fractal" a set of points are in a function.

More formally, the singularity spectrum 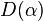$D(\alpha )$ of a function, $f(x)$ , is defined as:

$D(\alpha )=D_{F}\{x,\alpha (x)=\alpha \}$

Where $\alpha (x)$ is the function describing the Holder exponent, $\alpha (x)$ of $f(x)$ at the point $x$ . $D_{F}\{\cdot \}$ is the Hausdorff dimension of a point set.

References

van den Berg, J. C. (2004), Wavelets in Physics, Cambridge, ISBN 978-0-521-53353-9 .

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.

Singularity spectrum

See also

References