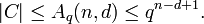Singleton bound

From Wikipedia, the free encyclopedia

In coding theory, the Singleton bound, named after Richard Collom Singleton, is a relatively crude bound on the size of a block code $C$ with block length $n$ , size $r$ and minimum distance $d$ .

Statement of the Bound

The minimum distance of a set $C$ of codewords of length $n$ is defined as

$d=\min _{{x,y\in C,x\neq y}}d(x,y)$

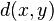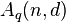where $d(x,y)$ is the Hamming distance between $x$ and $y$ . The expression $A_{{q}}(n,d)$ represents the maximum number of possible codewords in a q-ary block code of length $n$ and minimum distance $d$ .

Then the Singleton bound states that

$A_{q}(n,d)\leq q^{{n-d+1}}.$

Proof

First observe that there are $q^{n}$ many q-ary words of length $n$ , since each letter in such a word may take one of $q$ different values, independently of the remaining letters.

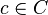Now let $C$ be an arbitrary q-ary block code of minimum distance $d$ . Clearly, all codewords $c\in C$ are distinct. If we delete the first 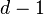$d-1$ letters of each codeword, then all resulting codewords must still be pairwise different, since all original codewords in $C$ have Hamming distance at least $d$ from each other. Thus the size of the code remains unchanged.

The newly obtained codewords each have length

$n-(d-1)=n-d+1$

and thus there can be at most

$q^{{n-d+1}}$

of them. Hence the original code $C$ shares the same bound on its size $|C|$ :

$|C|\leq A_{q}(n,d)\leq q^{{n-d+1}}.$

MDS codes

Block codes that achieve equality in Singleton bound are called MDS (maximum distance separable) codes. Examples of such codes include codes that have only one codeword (minimum distance n), codes that use the whole of $(F_{{q}})^{{n}}$ (minimum distance 1), codes with a single parity symbol (minimum distance 2) and their dual codes. These are often called trivial MDS codes.

In the case of binary alphabets, only trivial MDS codes exist.^[1]

Examples of non-trivial MDS codes include Reed-Solomon codes and their extended versions.^[2]

Notes

↑ see e.g. Vermani (1996), Proposition 9.2.
↑ see e.g. MacWilliams and Sloane, Ch. 11.

References

R.C. Singleton (1964). "Maximum distance q-nary codes". IEEE Trans. Inf. Theory 10 (2): 116–118. doi:10.1109/TIT.1964.1053661.

Further reading

J.H. van Lint (1992). Introduction to Coding Theory. GTM 86 (2nd ed.). Springer-Verlag. p. 61. ISBN 3-540-54894-7.
F.J. MacWilliams; N.J.A. Sloane (1977). The Theory of Error-Correcting Codes. North-Holland. pp. 33,37. ISBN 0-444-85193-3. Cite uses deprecated parameters (help)
Niederreiter, Harald; Xing, Chaoping (2001). "6. Applications to algebraic coding theory". Rational points on curves over finite fields. Theory and Applications. London Mathematical Society Lecture Note Series 285. Cambridge: Cambridge University Press. ISBN 0-521-66543-4. Zbl 0971.11033.
L. R. Vermani: Elements of algebraic coding theory, Chapman & Hall, 1996.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.