Silverman–Toeplitz theorem

From Wikipedia, the free encyclopedia

In mathematics, the Silverman–Toeplitz theorem, first proved by Otto Toeplitz, is a result in summability theory characterizing matrix summability methods that are regular. A regular matrix summability method is a matrix transformation of a convergent sequence which preserves the limit.

An infinite matrix 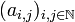$(a_{{i,j}})_{{i,j\in {\mathbb {N}}}}$ with complex-valued entries defines a regular summability method if and only if it satisfies all of the following properties

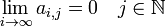$\lim _{{i\to \infty }}a_{{i,j}}=0\quad j\in {\mathbb {N}}$ (every column sequence converges to 0)

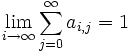$\lim _{{i\to \infty }}\sum _{{j=0}}^{{\infty }}a_{{i,j}}=1$ (the row sums converge to 1)

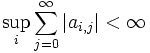$\sup _{{i}}\sum _{{j=0}}^{{\infty }}\vert a_{{i,j}}\vert <\infty$ (the absolute row sums are bounded).

References

Toeplitz, Otto (1911) "Über die lineare Mittelbildungen." Prace mat.-fiz., 22, 113–118 (the original paper in German)
Silverman, Louis Lazarus (1913) "On the definition of the sum of a divergent series." University of Missouri Studies, Math. Series I, 1–96

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.