Shrikhande graph
| Shrikhande graph | |
|---|---|
 The Shrikhande graph | |
| Named after | S. S. Shrikhande |
| Vertices | 16 |
| Edges | 48 |
| Radius | 2 |
| Diameter | 2 |
| Girth | 3 |
| Automorphisms | 192 |
| Chromatic number | 4 |
| Chromatic index | 6 |
| Properties |
Strongly regular Hamiltonian Symmetric Eulerian Integral |
In the mathematical field of graph theory, the Shrikhande graph is a named graph discovered by S. S. Shrikhande in 1959.[1][2] It is a strongly regular graph with 16 vertices and 48 edges, with each vertex having a degree of 6.
Construction
The Shrikhande graph can be constructed as a Cayley graph, where the vertex set is 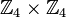 , and where two vertices are adjacent if and only if the difference is in
, and where two vertices are adjacent if and only if the difference is in  .
.
Properties
In the Shrikhande graph, any two vertices I and J have two distinct neighbors in common (excluding the two vertices I and J themselves), which holds true whether or not I is adjacent to J. In other words, its parameters for being strongly regular are: {16,6,2,2}, with 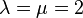 , this equality implying that the graph is associated with a symmetric BIBD. It shares these parameters with a different graph, the 4×4 rook's graph. The 4×4 square grid is the only square grid for which the parameters of the rook's graph are NOT unique, but are shared with a non-rook's graph, namely the Shrikhande graph. [2][3]
, this equality implying that the graph is associated with a symmetric BIBD. It shares these parameters with a different graph, the 4×4 rook's graph. The 4×4 square grid is the only square grid for which the parameters of the rook's graph are NOT unique, but are shared with a non-rook's graph, namely the Shrikhande graph. [2][3]
The Shrikhande graph is locally hexagonal; that is, the neighbors of each vertex form a cycle of six vertices. As with any locally cyclic graph, the Shrikhande graph is the 1-skeleton of a Whitney triangulation of some surface; in the case of the Shrikhande graph, this surface is a torus in which each vertex is surrounded by six triangles.[4] Thus, the Shrikhande graph is a toroidal graph. The dual of this embedding is the Dyck graph, a cubic symmetric graph.
The Shrikhande graph is not a distance-transitive graph. It is the smallest distance-regular graph that is not distance-transitive.[5]
The automorphism group of the Shrikhande graph is of order 192. It acts transitively on the vertices, on the edges and on the arcs of the graph. Therefore the Shrikhande graph is a symmetric graph.
The characteristic polynomial of the Shrikhande graph is : 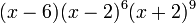 . Therefore the Shrikhande graph is an integral graph: its spectrum consists entirely of integers.
. Therefore the Shrikhande graph is an integral graph: its spectrum consists entirely of integers.
Gallery
-

The Shrikhande graph is a toroidal graph.
-
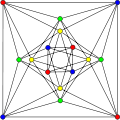
The chromatic number of the Shrikhande graph is 4.
-

The chromatic index of the Shrikhande graph is 6.
-
The Shrikhande graph drawn symmetrically.
-

The Shrikhande graph is Hamiltonian.
Notes
- ↑ Weisstein, Eric W., "Shrikhande Graph", MathWorld.
- ↑ 2.0 2.1 Shrikhande, S. S. (1959), "The uniqueness of the L2 association scheme", Annals of Mathematical Statistics 30: 781–798, JSTOR 2237417.
- ↑ Harary, F. (1972), "Theorem 8.7", Graph Theory, Massachusetts: Addison-Wesley, p. 79.
- ↑ Brouwer, A. E. Shrikhande graph.
- ↑ Brouwer, A. E.; Cohen, A. M.; Neumaier, A. (1989), Distance-Regular Graphs, New York: Springer-Verlag, pp. 104–105 and 136.
References
- Holton, D. A.; Sheehan, J. (1993), The Petersen Graph, Cambridge University Press, p. 270, ISBN 0-521-43594-3.
External links
- The Shrikhande Graph, Peter Cameron, August 2010.