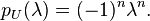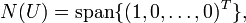Shift matrix

From Wikipedia, the free encyclopedia

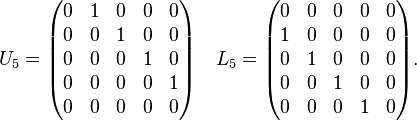
In mathematics, a shift matrix is a binary matrix with ones only on the superdiagonal or subdiagonal, and zeroes elsewhere. A shift matrix U with ones on the superdiagonal is an upper shift matrix. The alternative subdiagonal matrix L is unsurprisingly known as a lower shift matrix. The (i,j):th component of U and L are

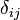$U_{{ij}}=\delta _{{i+1,j}},\quad L_{{ij}}=\delta _{{i,j+1}},$

where $\delta _{{ij}}$ is the Kronecker delta symbol.

For example, the 5×5 shift matrices are

$U_{5}={\begin{pmatrix}0&1&0&0&0\\0&0&1&0&0\\0&0&0&1&0\\0&0&0&0&1\\0&0&0&0&0\end{pmatrix}}\quad L_{5}={\begin{pmatrix}0&0&0&0&0\\1&0&0&0&0\\0&1&0&0&0\\0&0&1&0&0\\0&0&0&1&0\end{pmatrix}}.$

Clearly, the transpose of a lower shift matrix is an upper shift matrix and vice versa.

Premultiplying a matrix A by a lower shift matrix results in the elements of A being shifted downward by one position, with zeroes appearing in the top row. Postmultiplication by a lower shift matrix results in a shift left. Similar operations involving an upper shift matrix result in the opposite shift.

Clearly all shift matrices are nilpotent; an n by n shift matrix S becomes the null matrix when raised to the power of its dimension n.

Properties

Let L and U be the n by n lower and upper shift matrices, respectively. The following properties hold for both U and L. Let us therefore only list the properties for U:

det(U) = 0
trace(U) = 0
rank(U) = n−1
The characteristic polynomials of U is

$p_{U}(\lambda )=(-1)^{n}\lambda ^{n}.$

Uⁿ = 0. This follows from the previous property by the Cayley–Hamilton theorem.

The permanent of U is 0.

The following properties show how U and L are related:

L^T = U; U^T = L

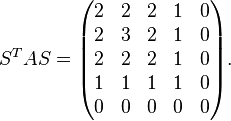
The null spaces of U and L are

$N(U)=\operatorname {span}\{(1,0,\ldots ,0)^{T}\},$

$N(L)=\operatorname {span}\{(0,\ldots ,0,1)^{T}\}.$

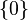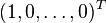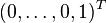The spectrum of U and L is $\{0\}$ . The algebraic multiplicity of 0 is n, and its geometric multiplicity is 1. From the expressions for the null spaces, it follows that (up to a scaling) the only eigenvector for U is $(1,0,\ldots ,0)^{T}$ , and the only eigenvector for L is $(0,\ldots ,0,1)^{T}$ .

For LU and UL we have

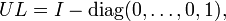
$UL=I-\operatorname {diag}(0,\ldots ,0,1),$

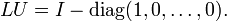
$LU=I-\operatorname {diag}(1,0,\ldots ,0).$

These matrices are both idempotent, symmetric, and have the same rank as U and L

L^n-aU^n-a + L^aU^a = U^n-aL^n-a + U^aL^a = I (the identity matrix), for any integer a between 0 and n inclusive.

Examples

$S={\begin{pmatrix}0&0&0&0&0\\1&0&0&0&0\\0&1&0&0&0\\0&0&1&0&0\\0&0&0&1&0\end{pmatrix}};\quad A={\begin{pmatrix}1&1&1&1&1\\1&2&2&2&1\\1&2&3&2&1\\1&2&2&2&1\\1&1&1&1&1\end{pmatrix}}.$

Then $SA={\begin{pmatrix}0&0&0&0&0\\1&1&1&1&1\\1&2&2&2&1\\1&2&3&2&1\\1&2&2&2&1\end{pmatrix}};\quad AS={\begin{pmatrix}1&1&1&1&0\\2&2&2&1&0\\2&3&2&1&0\\2&2&2&1&0\\1&1&1&1&0\end{pmatrix}}.$

Clearly there are many possible permutations. For example, $S^{{T}}AS$ is equal to the matrix A shifted up and left along the main diagonal.

$S^{{T}}AS={\begin{pmatrix}2&2&2&1&0\\2&3&2&1&0\\2&2&2&1&0\\1&1&1&1&0\\0&0&0&0&0\end{pmatrix}}.$

References

Shift Matrix - entry in the Matrix Reference Manual

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.

Shift matrix

Properties

Examples

See also

References