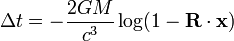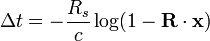Shapiro delay

From Wikipedia, the free encyclopedia

The Shapiro time delay effect, or gravitational time delay effect, is one of the four classic solar system tests of general relativity. Radar signals passing near a massive object take slightly longer to travel to a target and longer to return than they would if the mass of the object were not present.

History

The time delay effect was first noticed in 1964, by Irwin Shapiro. Shapiro proposed an observational test of his prediction: bounce radar beams off the surface of Venus and Mercury, and measure the round trip travel time. When the Earth, Sun, and Venus are most favorably aligned, Shapiro showed that the expected time delay, due to the presence of the Sun, of a radar signal traveling from the Earth to Venus and back, would be about 200 microseconds,^[1] well within the limitations of 1960s era technology.

The first tests, performed in 1966 and 1967 using the MIT Haystack radar antenna, were successful, matching the predicted amount of time delay.^[2] The experiments have been repeated many times since then, with increasing accuracy.

Calculating time delay

In a near-static gravitational field of moderate strength (say, of stars and planets, but not one of a black hole or close binary system of neutron stars) the effect may be considered as a special case of gravitational time dilation.The measured elapsed time of a light signal in a gravitational field is longer than it would be without the field, and for moderate strength near-static fields the difference is directly proportional to the classical gravitational potential, precisely as given by standard gravitational time dilation formulas.

Time delay due to light traveling around a single mass

For a signal going around a massive object, the time delay can be calculated as the following:

$\Delta t=-{\frac {2GM}{c^{3}}}\log(1-{\mathbf {R}}\cdot {\mathbf {x}})$

Here ${\mathbf {R}}$ is the unit vector pointing from the observer to the source, and

${\mathbf {x}}$ is the unit vector pointing from the observer to the gravitating mass M.

For the dot in 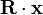${\mathbf {R}}\cdot {\mathbf {x}}$ , see Dot product.

The above formula can be rearranged like this:

$c\Delta t=-{\frac {2GM}{c^{2}}}\log(1-{\mathbf {R}}\cdot {\mathbf {x}})$

$\Delta x=-R_{s}\log(1-{\mathbf {R}}\cdot {\mathbf {x}})$

which is the extra distance the light has to travel, where 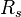$R_{s}$ is the Schwarzschild radius.

This is the same as:

$\Delta t=-{\frac {R_{s}}{c}}\log(1-{\mathbf {R}}\cdot {\mathbf {x}})$

or in PPN parameters

$\Delta t=-(1+\gamma ){\frac {R_{s}}{2c}}\log(1-{\mathbf {R}}\cdot {\mathbf {x}})$

I.e. twice the Newtonian prediction (with $\gamma =0$ ).^[3]

Interplanetary probes

Shapiro delay must be considered along with ranging data when trying to accurately determine the distance to interplanetary probes such as the Voyager and Pioneer spacecraft.

Shapiro delay of neutrinos and gravitational waves

From the near-simultaneous observations of neutrinos and photons from SN 1987A, we know that the Shapiro delay for high-energy neutrinos is the same as that for photons to within 10% (consistent with recent estimates of the neutrino mass which imply that those neutrinos were moving at very close to the speed of light). Since gravitational waves have not been directly detected, we don't have any data on the Shapiro delay for gravitational waves. In general relativity and other metric theories of gravity, the Shapiro delay for gravitational waves is expected to be the same as that for light (and neutrinos). However in theories such as Teves and other modified GR theories which reproduce Milgrom's law and avoid the need for dark matter, the Shapiro delay for gravitational waves is much smaller than that for neutrinos or photons.

References

↑ Irwin I. Shapiro (1964). "Fourth Test of General Relativity". Physical Review Letters 13 (26): 789–791. Bibcode:1964PhRvL..13..789S. doi:10.1103/PhysRevLett.13.789.
↑ Irwin I. Shapiro, Gordon H. Pettengill, Michael E. Ash, Melvin L. Stone, William B. Smith, Richard P. Ingalls, and Richard A. Brockelman (1968). "Fourth Test of General Relativity: Preliminary Results". Physical Review Letters 20 (22): 1265–1269. Bibcode:1968PhRvL..20.1265S. doi:10.1103/PhysRevLett.20.1265.
↑ Elena V. Pitjeva: Tests of General Relativity from observations of planets and spacecraft -