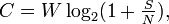Shannon–Weaver model

From Wikipedia, the free encyclopedia
The Shannon–Weaver model as portrayed in a report from the United States Office of Technology Assessment

The Shannon–Weaver model of communication has been called the "mother of all models."[1] It embodies the concepts of information source, message, transmitter, signal, channel, noise, receiver, information destination, probability of error, encoding, decoding, information rate, channel capacity, etc.

In 1948 Claude Elwood Shannon published A Mathematical Theory of Communication article in two parts in the July and October numbers of the Bell System Technical Journal.[2] In this fundamental work he used tools in probability theory, developed by Norbert Wiener, which were in their nascent stages of being applied to communication theory at that time. Shannon developed information entropy as a measure for the uncertainty in a message while essentially inventing what became known as the dominant form of "information theory."

The book co-authored with Warren Weaver, The Mathematical Theory of Communication, reprints Shannon's 1948 article and Weaver's popularization of it, which is accessible to the non-specialist.[3] Shannon's concepts were also popularized, subject to his own proofreading, in John Robinson Pierce's Symbols, Signals, and Noise.[4]

The term Shannon–Weaver model was widely adopted into social science fields such as education, organizational analysis, psychology, etc,however some critics have labeled it a "misleading misrepresentation of the nature of human communication", citing its simplicity and innability to consider context.[5] In engineering and mathematics, Shannon's theory is used more literally and is referred to as Shannon theory, or information theory.[6]

Shannon's capacity formula applied to the additive white Gaussian noise channel gives the Shannon–Hartley formula,

C=W\log _{{2}}(1+{\tfrac {S}{N}}),

where C is channel capacity measured in bits/second, W is the bandwidth in Hz, S is the signal level in watts across the bandwidth W, and N is the noise power in watts in the bandwidth W.

References

  1. ↑ David D. Woods and Erik Hollnagel (2005). Joint Cognitive Systems: Foundations of Cognitive Systems Engineering. Boca Raton, FL: Taylor & Francis. ISBN 0-8493-2821-7. 
  2. ↑ Claude Shannon (1948). "A Mathematical Theory of Communication". Bell System Technical Journal 27 (July and October): pp. 379–423, 623–656.  (July, October)
  3. ↑ Warren Weaver and Claude Elwood Shannon (1963). The Mathematical Theory of Communication. Univ. of Illinois Press. ISBN 0-252-72548-4. 
  4. ↑ John Robinson Pierce (1980). An Introduction to Information Theory: Symbols, Signals & Noise. Courier Dover Publications. ISBN 0-486-24061-4. 
  5. ↑ Daniel Chandler, The Transmission Model of communications 
  6. ↑ Sergio Verdü (2000). "Fifty years of Shannon theory". In Sergio Verdü and Steven W. McLaughlin. Information theory: 50 years of discovery. IEEE Press. pp. 13–34. ISBN 0-7803-5363-3. 


This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.