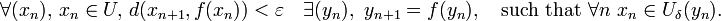Shadowing lemma

From Wikipedia, the free encyclopedia

A Shadowing lemma is also a fictional creature in the Discworld. See Shadowing lemma.

In the theory of dynamical systems, the shadowing lemma is a lemma describing the behaviour of pseudo-orbits near a hyperbolic invariant set. Informally, the theory states that every pseudo-orbit (which one can think of as a numerically computed trajectory with rounding errors on every step^[1]) stays uniformly close to some true trajectory (with slightly altered initial position) — in other words, a pseudo-trajectory is "shadowed" by a true one.

Formal statement

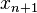Given a map f : X → X of a metric space (X, d) to itself, define a ε-pseudo-orbit (or ε-orbit) as a sequence $(x_{n})$ of points such that $x_{{n+1}}$ belongs to a ε-neighborhood of $f(x_{n})$ .

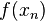Then, near a hyperbolic invariant set, the following statement holds:^[2] Let Λ be a hyperbolic invariant set of a diffeomorphism f. There exists a neighborhood U of Λ with the following property: for any δ > 0 there exists ε > 0, such that any (finite or infinite) ε-pseudo-orbit that stays in U also stays in a δ-neighborhood of some true orbit.

$\forall (x_{n}),\,x_{n}\in U,\,d(x_{{n+1}},f(x_{n}))<\varepsilon \quad \exists (y_{n}),\,\,y_{{n+1}}=f(y_{n}),\quad {\text{such that}}\,\,\forall n\,\,x_{n}\in U_{{\delta }}(y_{n}).$

References

↑ Weisstein, Eric W., "Shadowing Theorem", MathWorld.
↑ A. Katok, B. Hasselblatt, Introduction to the modern theory of dynamical systems, Theorem 18.1.2.

Scholarpedia article Shadowing Theorem

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.