Set-builder notation
In set theory and its applications to logic, mathematics, and computer science, set-builder notation is a mathematical notation for describing a set by stating the properties that its members must satisfy.[1] Forming sets in this manner is also known as set comprehension, set abstraction or as defining a set's intension. Although some simply refer to it as set notation, that label may be better reserved for the broader class of means of denoting sets.
Building sets
Let Φ(x) be a formula in which the variable x appears free. Set builder notation has the form {x : Φ(x)} or {x | Φ(x)}, denoting the set of all individuals in the universe of discourse satisfying the formula Φ(x), that is, the set whose members are every individual x such that Φ(x) is true: formally, the extension of the predicate. Φ(x) is here referred to as the rule. Sometimes the universe of discourse is established within the notation; writing  ,
,  or
or  establishes that the universe of discourse is
establishes that the universe of discourse is 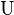 for purposes of the set being built. Set builder notation binds the variable x and must be used with the same care applied to variables bound by quantifiers. Unless specifically stated the variable is universally quantified over the rule, which means we include in the set all possible values for the variable for which the rule is true.
for purposes of the set being built. Set builder notation binds the variable x and must be used with the same care applied to variables bound by quantifiers. Unless specifically stated the variable is universally quantified over the rule, which means we include in the set all possible values for the variable for which the rule is true.
Examples:
-
 is a set holding the four numbers 3, 7, 15, and 31.
is a set holding the four numbers 3, 7, 15, and 31. -
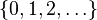 is the set of natural numbers.
is the set of natural numbers. -
 is the set of integers between 1 and 100 inclusive.
is the set of integers between 1 and 100 inclusive. -
 is the set containing 'a','b', and 'c'.
is the set containing 'a','b', and 'c'. -
 is the set
is the set  ,
, -
 is the set of all positive real numbers.
is the set of all positive real numbers. -
 is the set of (x,y) such that y is greater than 0 and less than f(x).
is the set of (x,y) such that y is greater than 0 and less than f(x). -
 is the set of all even natural numbers,
is the set of all even natural numbers, -
 is the set of rational numbers; that is, numbers that can be written as the ratio of two integers.
is the set of rational numbers; that is, numbers that can be written as the ratio of two integers. -
 Thus, e.g.,
Thus, e.g.,  , etc. (n.b.: in the case of sets, the order is not important;
, etc. (n.b.: in the case of sets, the order is not important;  could be used). As an example,
could be used). As an example, 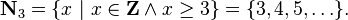
The ellipses means that the simplest interpretation should be applied for continuing the sequence. Should no terminating value appear to the right of the ellipses then the sequence is considered to be unbounded.
The vertical bar or colon is read as "such that", and it separates the variables list on the left from the rule for assigning values to those variables on the right. Oftentimes the rule on the right is a formal logic predicate. However it can be anything that is clear to readers including simple prose. When the meaning is clear the  and the rule may be omitted.
and the rule may be omitted.
When the rule is a predicate then formal logic connectors may be used within the rule. For example, the 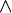 sign stands for and, requiring both clauses to the left of it and to the right of it to be 'true'. As another example, The
sign stands for and, requiring both clauses to the left of it and to the right of it to be 'true'. As another example, The  sign stands for "there exists" and is formally known as existential quantification. Sometimes multiple rules are given separated by a comma (,) or semicolon (;), in this case we take the rules in conjunction, i.e. we interpret the comma or semicolon to mean the same as
sign stands for "there exists" and is formally known as existential quantification. Sometimes multiple rules are given separated by a comma (,) or semicolon (;), in this case we take the rules in conjunction, i.e. we interpret the comma or semicolon to mean the same as 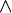 .
.
The  sign denotes set membership, and can be read as "member of" or informally as "in". In a predicate a clause of the form
sign denotes set membership, and can be read as "member of" or informally as "in". In a predicate a clause of the form 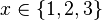 is either true or false, or when used as a constraint means that
is either true or false, or when used as a constraint means that  can only be one of the values 1, 2, or 3.
can only be one of the values 1, 2, or 3.
When the domain over which the set is defined is already clear it is not necessary to provide it within the rule clause. One could say something such as, "The universe of discourse can be taken to be the set of real numbers, where not specified inside the notation:" and then write:
-
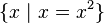 is the set
is the set 
Rather than the fuller form as shown in the original example given above.
One can also use an expression in the variable list. For example:
-
 is the set of odd integers.
is the set of odd integers. -
 creates a set of pairs, where each pair puts an integer into correspondence with an odd integer.
creates a set of pairs, where each pair puts an integer into correspondence with an odd integer. -
 is the set
is the set 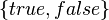 because the expression
because the expression  evaluates to either true or false given the various natural numbers.
evaluates to either true or false given the various natural numbers.
It is common in the literature to place the domain qualifiers with the variable expression.
-
 is the set
is the set  ,
,
Equivalent Builder Predicates means Equivalent Sets
Two sets are equal if and only if their set builder rules, including the domain specifiers, are logically equivalent. For example,  because, for any real number x, x2 = 1 if and only if |x| = 1. Note, had the domain specifiers in the rule stipulated complex numbers, mixed complex and real domains, or a number of other possibilities, the two sets in this example would not be equal.
because, for any real number x, x2 = 1 if and only if |x| = 1. Note, had the domain specifiers in the rule stipulated complex numbers, mixed complex and real domains, or a number of other possibilities, the two sets in this example would not be equal.
We can state this result more formally by considering two generic sets, namely, the set of elements created from set builder predicate P,
 ,
,
and the set of elements created by set builder predicate Q,
 .
.
Then sets A and B will be equal if
 .
.
Russell's paradox
Let  denote the set R of all sets S that do not contain themselves. Now lets ask a question about R. Does this set contain itself? I.e. can it be one of the elements S? If R does not contain itself, then according to the set builder rule it fits the criteria for being an S element, so it should be in R; however, if it is in R then it contains itself! We arrive at a contradiction. Lets take the opposite case, that R contains itself, then by definition it should not be in the set R. Another contradiction! According to the constructs of Whitehead's set theory, all elements are either in a set, or not in a set, but here using the same theory, Bertrand Russell shows an example of element, R which can not be either. The inconsistency in the existence of this set is known as Russell's paradox.
denote the set R of all sets S that do not contain themselves. Now lets ask a question about R. Does this set contain itself? I.e. can it be one of the elements S? If R does not contain itself, then according to the set builder rule it fits the criteria for being an S element, so it should be in R; however, if it is in R then it contains itself! We arrive at a contradiction. Lets take the opposite case, that R contains itself, then by definition it should not be in the set R. Another contradiction! According to the constructs of Whitehead's set theory, all elements are either in a set, or not in a set, but here using the same theory, Bertrand Russell shows an example of element, R which can not be either. The inconsistency in the existence of this set is known as Russell's paradox.
It is possible to avoid this paradox by restricting the richness in expressive power of the original set theory. To illustrate this in terms of our notation, let X = {x ∈ A | P(x)} denote the set of every element of A satisfying the predicate P(x). The canonical restriction on set builder notation asserts that X is a set only if A is already known to be a set. This restriction is codified in the axiom schema of separation present in standard axiomatic set theory. Note that this axiom schema excludes R from sethood.
Variations
Terms more complicated than a single variable
Another variation on set-builder notation replaces the single variable x with a term T which may include one or more variables, combined with functions acting on them. So instead of {x : Φ(x)}, we would have {T : Φ(x1 ... xn)}, where T is a term involving variables x1 through xn. For example:
- {2n : n ∈ N}, where N is the set of all natural numbers, is the set of all even natural numbers.
- {p/q : p,q ∈ Z, q≠0}, where Z is the set of all integers, is the set of all rational numbers (Q).
Z notation
In Z notation, the set of all x (in a universe of discourse A) satisfying the condition P(x) would be written 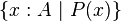 . In Z, an element x's set membership is written as
. In Z, an element x's set membership is written as  instead of
instead of 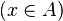 ; the vertical bar is used to indicate a predicate. Versions of set builder notation are also available in Z which allow for terms more complicated than a single variable, using a bullet to indicate the form of members of the set. So
; the vertical bar is used to indicate a predicate. Versions of set builder notation are also available in Z which allow for terms more complicated than a single variable, using a bullet to indicate the form of members of the set. So 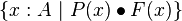 denotes the set of all values F(x), where x is in A and P(x) holds.
denotes the set of all values F(x), where x is in A and P(x) holds.
Parallels in programming languages
A similar notation available in a number of programming languages (notably Python and Haskell) is the list comprehension, which combines map and filter operations over one or more lists.
In Python, the set-builder's braces are replaced with square brackets, parentheses, or curly braces, giving list, generator, and set objects, respectively. Python uses an English based syntax. Haskell replaces the set-builder's braces with square brackets and uses symbols, including the standard set-builder vertical bar. Consider these examples given in set-builder notation, Python, and Haskell:
| Example 1 | Example 2 | |
|---|---|---|
| Set-builder |  |  |
| Python | {l for l in L} | {(k, x) for k in K for x in X if P(x)} |
| Haskell | [l | l <- ls] | [(k, x) | k <- ks, x <- xs, p x] |
The set builder notation and list comprehension notation are both instances of a more general notation known as monad comprehensions, which permits map/filter-like operations over any monad with a zero element.[2]
References
- ↑ Rosen, Kenneth (2007). Discrete Mathematics and its Applications (6th ed.). New York, NY: McGraw-Hill. pp. 111–112. ISBN 978-0-07-288008-3.
- ↑ Nils Schweinsberg (27 Nov 2010). "Fun with monad comprehensions". Retrieved 4 July 2011.