Serpentine curve

From Wikipedia, the free encyclopedia

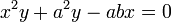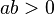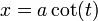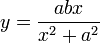A serpentine curve is a curve whose equation is of the form $x^{2}y+a^{2}y-abx=0$ , where $ab>0$ . Equivalently, it has a parametric representation $x=a\cot(t)$ , $y=b\sin(t)\cos(t)$ , or functional representation $y={\frac {abx}{x^{2}+a^{2}}}$ . Serpentine curves were studied by L'Hôpital and Huygens, and named and classified by Newton.