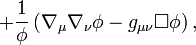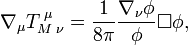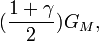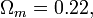Self-creation cosmology
| Part of a series on |
| Physical cosmology |
|---|
 |
|
Early universe
|
|
Expanding universe |
|
Structure formation
|
|
Future of universe |
|
Components |
|
Social impact |
|
Self-creation cosmology (SCC) theories are gravitational theories in which the mass of the universe is created out of its self-contained gravitational and scalar fields, as opposed to the theory of continuous creation cosmology or the steady state theory which depend on an extra 'creation' field.
History
As an alternative gravitational theory SCC is a non-standard cosmology in which the Brans-Dicke theory (BD) has been modified to allow for mass creation. It relaxes the requirement of the conservation of energy-momentum (or four-momentum) so the scalar field may interact directly with matter.
The original SCC paper (Barber, 1982) explored two toy theories, the first of which was rejected in that paper on the grounds of a gross violation of the equivalence principle. Brans (1987) also showed later that it was internally inconsistent. However, the second toy model has been much cited (62 to date) and has subsequently proved to be an early version of a new and comprehensive theory (2002).
A brief overview
Belayev (1999) proposed that in accordance with a conservation law the rest mass decrease leads to the energy liberation, which can create mass, though the solution of field equations brought in his paper needs in revision.
In the new Self-Creation Cosmology theory (henceforth referred to as just SCC) the modification of the Brans Dicke theory, which allows the creation of matter and energy, is constrained by the principle of the local conservation of energy. This has the effect that rest masses vary whereas the observed Newtonian Gravitation ’constant’ does not. Furthermore, there is a conformal equivalence between SCC and General Relativity in vacuo, which results in the predictions of the two theories being equal in the standard tests.
The predictions of GR and SCC are identical in all tests to date because there is a scalar field force acting on 'free falling particles' that in vacuo exactly compensates for the scalar field perturbation of GR space-time. As a consequence, in vacuo, SCC test particles follow the geodesics of General Relativity. Nevertheless, there are three types of experiment that are able to distinguish between the two theories.
A significant feature of SCC is that it is as consistent with cosmological constraints as the standard paradigm in the Cosmic Microwave Background anisotropies and primordial nucleo-synthesis. Unlike the standard model, however, it does not require the addition of the undiscovered physics of Inflation, dark non-baryonic matter, or unknown dark energy. On the other hand it does demand an exotic equation of state, which requires the presence of false vacuum energy at a moderate density that is determined by the field equations. As a result of this link between the false vacuum and space-time curvature the theory is able to interface gravitation and quantum theories without creating a ’Lambda’ problem. There is a problem fitting the distant Type Ia supernovae data as this theory requires them not to be standard candles over cosmological history but intrinsically fainter in the past.
In SCC there are two frames of interpretation of observational data, which depend on whether energy or energy-momentum is to be conserved and whether photons or atoms respectively are chosen as the invariant standards of measurement. In the former frame the universe is stationary and eternal with exponentially shrinking rulers and accelerating atomic clocks, while in the latter, and more familiar, frame the universe is 'freely coasting', and expands linearly from a Big Bang with rigid rulers and regular atomic clocks.
Such a strictly linearly expanding universe does not require Inflation to resolve the horizon problem, or the smoothness and flatness problems that exist in GR as they do not arise in the first place.
General self-creation cosmology theories
The GR gravitational field equation of all Self-Creation Cosmology theories is modified to explicitly include Mach's principle, following Brans-Dicke, by including the stress-energy tensor of a scalar field energy  :
:
![R_{{\mu \nu }}-{\frac 12}g_{{\mu \nu }}R={\frac {8\pi }\phi }\left[T_{{M\mu \nu }}+T_{{\phi \,\mu \nu }}\right]](/2014-wikipedia_en_all_02_2014/I/media/6/d/7/7/6d77a5d81a5cb487bd293518af7bd4de.png) ,
,
where  is the stress energy tensor describing the matter field. The scalar field
is the stress energy tensor describing the matter field. The scalar field
 , where
, where  is the Newtonian gravitational 'constant',
is the Newtonian gravitational 'constant',
is coupled to the large scale distribution of matter in motion, described by a field equation of the simplest general covariant form
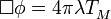 ,
,
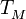 is the trace,
is the trace,  , of the stress energy
tensor describing all non-gravitational and non-scalar field energy. In the new SCC, the Brans Dicke parameter
, of the stress energy
tensor describing all non-gravitational and non-scalar field energy. In the new SCC, the Brans Dicke parameter 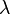 has been determined to be unity.
has been determined to be unity.
The BD field equation is modified in all these theories by the non-conservation of stress-energy, so the conservation equation does not apply,
 .
.
The new (2002) theory
An alternative to the principle of the conservation of energy-momentum is required, in order to constrain mass creation.
In the new SCC theory it is postulated that mass is created out of gravitational and scalar fields in accordance with the Principle of Mutual Interaction (PMI).
The PMI states that:
"The scalar field is a source for the matter-energy field if and only if the matter-energy field is a source for the scalar field."
As the source for the scalar field is the trace of the stress-energy tensor, the PMI is delivered by coupling this trace to the divergence of the stress-energy tensor. As a consequence relativistic energy such as light, which is trace free, still obeys the Equivalence Principle.
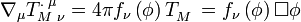 .
.
As a consequence photons still do traverse null-geodesics, at least in vacuo,
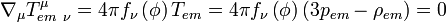 .
.
A detailed calculation yields:
 ,
,
so
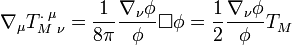 .
.
In the new theory energy is locally conserved when measured in a particular, preferred, frame of reference that is selected by Mach’s principle, which is the Centre of Mass (CoM) of the system. The Jordan conformal frame of the theory is defined to be that in which rest mass includes gravitational potential energy. Such energy is defined and measured in that CoM frame of reference.
This local conservation of energy requires the energy expended in lifting an object against a gravitational field to be translated into an increase in its rest mass. If  is the dimensionless Newtonian gravitational potential, defined by a measurement of acceleration in a local experiment in a frame of reference co-moving with the Centre of Mass frame (CoM), so
is the dimensionless Newtonian gravitational potential, defined by a measurement of acceleration in a local experiment in a frame of reference co-moving with the Centre of Mass frame (CoM), so
and normalized so that
then the local conservation of energy requires
where 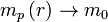 as
as 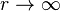 .
.
Violation of the equivalence principle
The effect of the non-conservation of the stress-energy tensor is that every non-relativistic particle experiences a scalar field force that behaves in a similar way to the gravitational force experienced by a supported particle and which is therefore confused with it.
This force is calculated to be 1/3 the strength of the gravitational force acting on a supported particle but in the opposite, anti-gravity, direction.
According to SCC the Newtonian gravitational constant  , as measured in a Cavendish type experiment, is a compilation of the effect of the curvature of space time, with its corresponding
, as measured in a Cavendish type experiment, is a compilation of the effect of the curvature of space time, with its corresponding  , and the action of the scalar field. So the combined Newtonian gravitational constant
experienced by a particle with mass is
, and the action of the scalar field. So the combined Newtonian gravitational constant
experienced by a particle with mass is
Note that  and
and  refer to the total gravitational accelerations experienced in physical
experiments by atomic particles and photons respectively.
refer to the total gravitational accelerations experienced in physical
experiments by atomic particles and photons respectively.
Different particles all 'fall at the same acceleration', except there is a perturbation caused by the pressure term in the stress-energy tensor. That notwithstanding, because in normal laboratory conditions 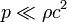 , detailed calculations , , have shown that in tests this theory predicts an observable violation of the Equivalence Principle of only one part in
, detailed calculations , , have shown that in tests this theory predicts an observable violation of the Equivalence Principle of only one part in  , i.e. three orders of magnitude smaller than the present experimental limits.
, i.e. three orders of magnitude smaller than the present experimental limits.
Gravitational red shift
The local conservation of energy, and the consequential variation in rest mass, demand that gravitational mass is treated under the de Broglie wave theory. Mass is defined by the DeBroglie frequency of that particle. The red shift caused by the curvature of space-time, a time dilation expressed by the metric component  , is suffered not only by the photon but also by the atom with which it interacts and is thus undetectable. The red shift that is detectable is caused by the increase in rest mass that fundamental particles undergo when raised to the higher level. Gravitational red shift in this theory is interpreted not as a loss of gravitational potential energy by the photon but as a gain of gravitational potential energy by the apparatus measuring it. The red shift predicted is hence equal to the difference in Newtonian potential and thus identical with that of GR as confirmed in the Pound-Rebka experiment.
, is suffered not only by the photon but also by the atom with which it interacts and is thus undetectable. The red shift that is detectable is caused by the increase in rest mass that fundamental particles undergo when raised to the higher level. Gravitational red shift in this theory is interpreted not as a loss of gravitational potential energy by the photon but as a gain of gravitational potential energy by the apparatus measuring it. The red shift predicted is hence equal to the difference in Newtonian potential and thus identical with that of GR as confirmed in the Pound-Rebka experiment.
Two conformal frames of measurement
These equations have been cast in the Jordan frame in which particle masses vary and it is a 'standard' photon (carefully defined) that is the measure of energy/mass, length and time. The theory may also be conformally transformed into its Einstein frame in which particle masses are constant, consequently atoms become the measure of mass/energy, length and time. The conformal transformation of a metric into a physically equivalent alternative is described by
Now mass is conformally transformed according to
where 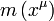 is the mass of a fundamental particle in the Jordan Frame and
is the mass of a fundamental particle in the Jordan Frame and 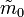 its invariant mass in the Einstein Frame. Therefore the local conservation of energy in the SCC Jordan Frame requires
its invariant mass in the Einstein Frame. Therefore the local conservation of energy in the SCC Jordan Frame requires
There is a conformal equivalence between SCC and GR in vacuo when the Einstein frame Lagrangian becomes that of canonical GR. This results in an experimental degeneracy as the paths of geodesics through vacuum are identical in both theories. Although the extra scalar field perturbs the GR metric, and in addition the violation of the equivalence principle perturbs the geodesics of massive particles within that space-time, it is found that the two effects cancel each other out.
The action principle
The following Lagrangian density contains the complete description of the SCC theory.
The Lagrangian density in the Jordan conformal frame is that of a scalar tensor theory with
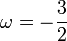 :
:
which produces the gravitational field equation given in the next section.
In this frame both
 and
and
 vary in such a way that
vary in such a way that
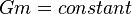 .
.
Note: In invariant conformal gravity theories the dimensionless 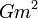 is invariant under transformation and mass variation is merely a consequence of the coordinate transformation. In the Jordan frame of SCC, which is a non-invariant conformal theory, the mass physically increases with gravitational potential as a result of the work done on it by lifting it against the gravitational potential gradient. As a consequence it is
is invariant under transformation and mass variation is merely a consequence of the coordinate transformation. In the Jordan frame of SCC, which is a non-invariant conformal theory, the mass physically increases with gravitational potential as a result of the work done on it by lifting it against the gravitational potential gradient. As a consequence it is  that remains invariant under the conformal transformation.
that remains invariant under the conformal transformation.
In the Einstein conformal frame, in which m is constant (and therefore, as Gm is constant, so is
 and
and  ), the conformal dual is given by:
), the conformal dual is given by:
which reduces down to the canonical GR Lagrangian density in vacuo, [ ]:
]:
Note that, as the stress-energy tensor is not conserved in the Jordan conformal frame, then the Principle of least action has to be applied to the Einstein conformal frame and only then transformed into the Jordan conformal frame.
The relationship corresponding to the GR conservation equation, derived from varying  , does not now exist because
, does not now exist because  does not appear in the Einstein conformal frame Lagrangian density, it is decoupled from the scalar field. The novel feature of the new SCC, distinguishing it from a simple conformal transformation of GR, is that Mach's Principle can now be fully incorporated in the Jordan conformal frame by requiring the scalar field equation (below) to hold, which retains the scalar field coupling to the distribution of matter and thereby produces the creation field equation (below).
does not appear in the Einstein conformal frame Lagrangian density, it is decoupled from the scalar field. The novel feature of the new SCC, distinguishing it from a simple conformal transformation of GR, is that Mach's Principle can now be fully incorporated in the Jordan conformal frame by requiring the scalar field equation (below) to hold, which retains the scalar field coupling to the distribution of matter and thereby produces the creation field equation (below).
The general field equations
The Principle of least action is applied in the SCC Einstein Frame and then the above conformal transformation into the Jordan Frame is used to give rise to the following set of equations:
The scalar field equation
The gravitational field equation
And the creation field equation, which replaces the GR conservation equation
The Machian frame of reference
These field equations are manifestly covariant, i.e. there is no preferred frame of reference or absolute time. However, in order to solve them one has to adopt a specific coordinate system; that is the CoM of the system in the spherically symmetric One Body Case, or that of the comoving fluid of the cosmological solution. This latter frame of reference may be identified with that in which the Cosmic microwave background radiation is globally isotropic.
In these CoM frames of reference there is a specific coordinate time, as indeed there is in the equivalent GR solutions (The null infinity time and cosmological time of GR respectively). Moreover, in the Jordan conformal frame, these solutions are not only in the frame of reference selected by Mach's principle , but in SCC, with this preferred foliation of space-time, they also locally conserve energy .
Falsifiable tests of the theory
As stated above, in vacuo the new theory is conformally equivalent to canonical GR so that test particles follow the geodesics of GR in solar system experiments. As all tests of GR to date measure the free-falling trajectories (GR geodesics) of test particles and photons through a vacuum, they cannot distinguish between GR or SCC. This degeneracy, , may be resolved by three further definitive experiments in which the predictions of the two theories do differ.
One of them, the Gravity Probe B geodetic precession, which measures the precessions of four accurate orbiting gyroscopes, is being evaluated in 2007; SCC predicts 2/3 that of the GR N-S precession, i.e. 4.4096 arcsec/yr. whereas the frame-dragging or gravitomagnetic E-W precession prediction is the same as that of GR i.e. 0.0409 arcsec/yr. The first results of this experiment were published at the American Physical Society Meeting on the 14th April 2007. While unforeseen errors are still being determined through 2007 the geodetic precession measurement of 6.6 arcsec/yr, which is within 1% of the GR prediction, is fatal to the present form of SCC.
The reason that one of these GP-B tests predicts the same result as GR, whereas the other GP-B test does not, is due to the two different formulas used in the predictions. In the frame dragging prediction, there is a term
where 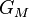 is the gravitational parameter that enters into the field equation and defines the metric, which in a non-metric or semi-metric theory is not necessarily the same as
is the gravitational parameter that enters into the field equation and defines the metric, which in a non-metric or semi-metric theory is not necessarily the same as  , the Newtonian gravitational constant.
, the Newtonian gravitational constant.
Now in GR 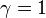 and we do have
and we do have
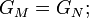
whereas in SCC, 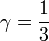 , however we also have
, however we also have
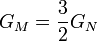 , which compensates for that difference in
, which compensates for that difference in  with the GR value, so this prediction of SCC is equal to its GR equivalent.
with the GR value, so this prediction of SCC is equal to its GR equivalent.
Now  is the amount of space curvature per unit GM and in the geodetic precession, which directly measures curvature, the corresponding term is
is the amount of space curvature per unit GM and in the geodetic precession, which directly measures curvature, the corresponding term is
so the corresponding geodetic precession is 5/6 the GR prediction.
However, this is not the end of the matter for according to SCC the satellite is not in free fall, it is being accelerated by the scalar field force. This introduces an extra Thomas precession of 1/6 the GR prediction. This extra precession has to be subtracted thus leaving a total SCC geodetic precession in a N-S direction of 2/3 the GR prediction or just 4.4096 arcsec/yr.
A second test asks the question: "Do photons and particles 'fall at the same rate' and uses the fact that the Earth is in free fall around the Sun, with a radial acceleration of about 0.01 m/s².
For example, the laser beams of the LIGO gravity wave telescope travel horizontally along two orthogonal 4km tunnels and are then reflected back to be re-combined at an interferometer at source. For this experimental test the interferometer might be adapted so that one beam could be returned immediately by an additional mirror to give it a negligible path length and then compared with the other beam that had travelled 8 km. The theory predicts that the two beams would then be displaced relative to each other in a direction towards the Sun by an amount
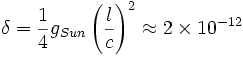 m/s²,
m/s²,
where 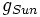 is the Newtonian gravitational acceleration of the Earth towards the Sun.
is the Newtonian gravitational acceleration of the Earth towards the Sun.
Although the LIGO interferometers can measure a longitudinal displacement to an accuracy of 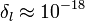 m/s², the transverse position of the LIGO beam is not presently known accurately enough to test this prediction. (Kip Thorne: private communication)
m/s², the transverse position of the LIGO beam is not presently known accurately enough to test this prediction. (Kip Thorne: private communication)
The third type of test poses the following question; "Is there a limit to the Casimir force that is dependent on space-time curvature?" This question arises from the real vacuum solutions of the scalar potential, which yield small non-zero densities if the curvature is non-zero. The Jordan frame requires a definite, small, negative vacuum density of virtual photons whereas the Einstein frame requires a small positive density of 'upwards' accelerating virtual particles. The theory thereby suggests a natural connection between gravitational theory and quantum expectations of the vacuum. These virtual densities are coupled to curvature and approach zero simultaneously as curvature asymptotically tends to flatness. Thus it seems that SCC predicts a limit to the Casimir force as a function of space-time curvature that may be detectable. A rough calculation, dependent on the sensitivity of the apparatus, indicates that a detection of a rounding off of the maximum Casimir force may be made in the solar system somewhere between the orbits of Jupiter and Saturn. This is also the distance where the Pioneer Anomaly starts being detectable.
The cosmological solution
In the cosmological solution of SCC the density is not in general zero, therefore the theory does differ from canonical GR, and is highly determined. The theory is therefore readily falsifiable, yet interestingly it is found that SCC is concordant with present cosmological constraints. Moreover, it is concordant without requiring the unverified process of Inflation, unknown dark energy, or exotic non-baryonic dark matter.
The normal Einstein conformal frame cosmological solution
In the Einstein conformal frame the universe is closed and expands in a strictly linear fashion from a Big Bang gravitational singularity. In this frame atomic masses are constant, rulers are fixed and clocks are regular.
The spatial geometry of the universe is conformally flat. As the Cosmic microwave background radiation anisotropy data is angular in nature, and conformal transformations are angle preserving, then the COBE and WMAP data, which are consistent with a spatially flat universe, are also consistent with the conformally flat spatial geometry of SCC. Indeed, such a closed and finite conformally flat geometry may be more consistent with that data, as the power spectrum of the cosmic microwave background radiation anisotropy is observed to suffer from a deficient quadrupole.
The matter content of the universe is created out of the scalar field, therefore the cosmological density parameters are precisely determined:
the total matter (visible and Dark) density parameter
and the false vacuum energy density parameter
which make up the total density.
In particular, as an example of a freely coasting model , in which the universe expands strictly linearly with time , SCC clears basic constraints on nucleosynthesis, with a baryonic matter density of
so there is no need to invoke unknown exotic non-baryonic DM. According to this theory the DM is originally baryonic in nature, this poses the major question for the theory: "In what form is this dark baryonic matter today?"
The Jordan conformal frame cosmological solution
In the Jordan conformal frame the cosmological solution is closed, static (but dynamically evolving), eternal and singularity free. In this frame rulers 'shrink' (relative to the peak wavelength of the CMB) and atomic clocks 'speed up' (relative to time measured by the peak frequency of the CMB) as their atoms exponentially gain mass with cosmological time .
Philosophical problems associated with 'an origin' thus disappear.
Clock drift
Finally, SCC predicts a cosmological 'clock drift' between atomic clock time and ephemeris time. Consequentially, in some methods of measurement distant spacecraft should appear to suffer a sunwards acceleration equal to cH, as indeed seems to be observed in the Pioneer anomaly.
External links and references
(Note: some of these links sometimes require accessing twice before the link is made.)
- Barber, G.A., 1982, Gen Relativ Gravit. 14, 117. On Two Self Creation Cosmologies.
- Singh, T. & Singh, T. :1984, Astrophysics and Space Science 102, 1. Some general results in self-creation cosmologies.
- Pimentel, L.O. : 1985, Astrophysics and Space Science 116, 2. Exact self-creation cosmological solutions.
- Brans, C.H. :1987, Gen Relativ Gravit.19, 949. Consistency of field equations in self-creation cosmologies
- Reddy, D.R.K. & Venkateswarlu, R. : 1987, Astrophysics and Space Science 136, p. 191-194. Birkhoff-type theorem in the scale-covariant theory of gravitation
- Soleng, Harald H. : 1987, Astrophysics and Space Science 139, 1. Self-creation cosmological solutions.
- Wolf, C.: 1988, PhyS...38..129W Can inflation take place in a closed universe admitting creation?
- Abdel-Rahman, A.M.M. :1992, Astrophysics and Space Science 189, 1. Singularity-free self-creation cosmology.
- Sanyasiraju1, Y. & Rao, V. :1992, Astrophysics and Space Science 189, 1. Exact Bianchi-type VIII and IX models in the presence of the self-creation theory of cosmology
- Abdussattar & Vishwakarma, R. G. : 1997, Classical and Quantum Gravity 14 pp 945-953 Some FRW models with variable G and Λ.
- Belayev, W.B., 1999, The Cosmological model in 5-D, stationarity, yes or no, gr-qc/9903016 (ArXiv)
- Mohanty, G. & Mishra, B. : 2001, Theoretical and Applied Mechanics 26, pgs 71 – 82. Dissipation of general viscous fluid distribution in Einstein and Barber theories.
- Mohanty, G. & Mishra, B. : 2002, Astrophysics and Space Science 281,3. Vacuum cosmological models in Einstein and Barber theories.
- Barber, G.A., Astrophysics and Space Science, (2002) 282,4 pgs 683-730. A New Self Creation Cosmology.
- Blaschke, D. & Dabrowski, M., 2004, Conformal relativity versus Brans-Dicke and superstring theories
- Barber, G.A., 2005, Self Creation Cosmology - An Alternative Gravitational Theory, one chapter of 'Horizons in World Physics, Volume 247: New Developments in Quantum Cosmology Research', Nova Science Publishers, Inc. New York. Also (ArXiv)
- Barber, G.A., 2006, Astrophys Space Sci (2006) 305:169–176, DOI 10.1007/s10509-006-9056-5, Resolving the Degeneracy: Experimental tests of the New Self Creation Cosmology and a heterodox prediction for Gravity Probe B. Also (ArXiv)
- Barber, G.A., The Principles of Self Creation Cosmology and its Comparison with General Relativity(ArXiv)
- Barber, G.A., 2003, The derivation of the coupling constant in the new Self Creation Cosmology(ArXiv)
- Barber, G.A., 2004 , The Self Creation challenge to the cosmological concordance model(ArXiv)
- Dabrowski, M., Denkiewicz, T. & Blaschke, D., 2005, "The conformal status of ω = −3/2 Brans-Dicke cosmology.
- Venkateswarlu, R., Pavan Kumar K.: 2006, Higher Dimensional FRW Cosmological Models in Self-Creation Theory, Astrophysics and Space Science 301, 1-4.
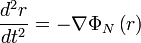
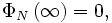
![m_{p}(x^{\mu })=m_{0}\exp[\Phi _{N}\left(x^{\mu }\right)],](/2014-wikipedia_en_all_02_2014/I/media/0/e/6/2/0e6214af1d49d88c72eeeb1415650e9a.png)



![\Omega =\exp \left[\Phi _{N}\left(x^{\mu }\right)\right].](/2014-wikipedia_en_all_02_2014/I/media/b/6/3/3/b633afdd4e24ca03f1cfe4210b8629a1.png)
![L^{{SCC}}[g,\phi ]={\frac {{\sqrt {-g}}}{16\pi }}\left(\phi R+{\frac {3}{2\phi }}g^{{\mu \nu }}\nabla _{{\mu }}\phi \nabla _{{\nu }}\phi \right)+L_{{matter}}^{{SCC}}[g,\phi ],](/2014-wikipedia_en_all_02_2014/I/media/8/c/e/1/8ce15af24c5c0d55fae8313ee781609c.png)
![L^{{SCC}}[{\tilde {g}},{\tilde {\phi }}]={\frac {{\sqrt {-{\tilde {g}}}}}{16\pi G_{{N}}}}{\tilde {R}}+{\tilde {L}}_{{matter}}^{{SCC}}[{\tilde {g}}]+{\frac {3{\sqrt {-{\tilde {g}}}}}{8\pi G_{{N}}}}{\tilde {\square }}{\tilde {\Phi }}_{{N}}\left({\tilde {x}}^{{\mu }}\right),](/2014-wikipedia_en_all_02_2014/I/media/0/a/0/b/0a0b88a7984c167b956c081b6c82b9b3.png)
![L^{{SCC}}[{\tilde {g}},{\tilde {\phi }}]={\frac {{\sqrt {-{\tilde {g}}}}}{16\pi G_{{N}}}}{\tilde {R}}+{\tilde {L}}_{{matter}}^{{SCC}}[{\tilde {g}}].](/2014-wikipedia_en_all_02_2014/I/media/c/5/6/1/c561588105739446bb2201a0b0769585.png)