Self-adjoint
In mathematics, an element x of a star-algebra is self-adjoint if 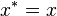 .
.
A collection C of elements of a star-algebra is self-adjoint if it is closed under the involution operation. For example, if 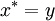 then since
then since  in a star-algebra, the set {x,y} is a self-adjoint set even though x and y need not be self-adjoint elements.
in a star-algebra, the set {x,y} is a self-adjoint set even though x and y need not be self-adjoint elements.
In functional analysis, a linear operator A on a Hilbert space is called self-adjoint if it is equal to its own adjoint A* and that the domain of A is the same as that of A*. See self-adjoint operator for a detailed discussion. If the Hilbert space is finite-dimensional and an orthonormal basis has been chosen, then the operator A is self-adjoint if and only if the matrix describing A with respect to this basis is Hermitian, i.e. if it is equal to its own conjugate transpose. Hermitian matrices are also called self-adjoint.
See also
- Symmetric matrix
- Hermitian
References
- Reed, M.; Simon, B. (1972). Methods of Mathematical Physics. Vol 2. Academic Press.
- Teschl, G. (2009). Mathematical Methods in Quantum Mechanics; With Applications to Schrödinger Operators. Providence: American Mathematical Society.