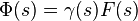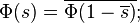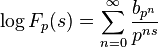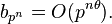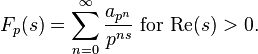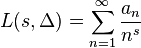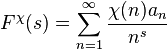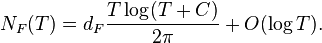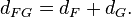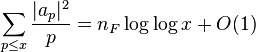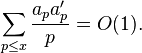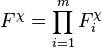Selberg class
In mathematics, the Selberg class is an axiomatic definition of a class of L-functions. The members of the class are Dirichlet series which obey four axioms that seem to capture the essential properties satisfied by most functions that are commonly called L-functions or zeta functions. Although the exact nature of the class is conjectural, the hope is that the definition of the class will lead to a classification of its contents and an elucidation of its properties, including insight into their relationship to automorphic forms and the Riemann hypothesis. The class was defined by Atle Selberg in (Selberg 1992).
Definition
The formal definition of the class S is the set of all Dirichlet series
absolutely convergent for Re(s) > 1 that satisfy four axioms:
- Analyticity: the function (s − 1)mF(s) is an entire function of finite order for some non-negative integer m;
- Ramanujan conjecture: a1 = 1 and
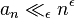 for any ε > 0;
for any ε > 0; - Functional equation: there is a gamma factor of the form
where φ is real, Q real and positive, Γ is the gamma function, the ω1 real and positive, and the μi complex with non-negative real part, so that the function
satisfies
- Euler product: F(s) can be written as a product over primes:
with
and, for some θ < 1/2,
Comments on definition
The condition that the real part of μi be non-negative is because there are known L-functions that do not satisfy the Riemann hypothesis when μi is negative. Specifically, there are Maass cusp forms associated with exceptional eigenvalues, for which the Ramanujan–Peterssen conjecture holds, and have a functional equation, but do not satisfy the Riemann hypothesis.
The condition that θ < 1/2 is important, as the θ = 1/2 case includes the Dirichlet eta-function, which violates the Riemann hypothesis.[1]
It is a consequence of 4. that the an are multiplicative and that
Examples
The prototypical example of an element in S is the Riemann zeta function.[2] Another example, is the L-function of the modular discriminant Δ
where  and τ(n) is the Ramanujan tau function.[3] Additionally, if F is in S and χ is a primitive Dirichlet character, then Fχ defined by
and τ(n) is the Ramanujan tau function.[3] Additionally, if F is in S and χ is a primitive Dirichlet character, then Fχ defined by
is also in S.
All known examples are automorphic L-functions, and the reciprocals of Fp(s) are polynomials in p−s of bounded degree.[4]
Basic properties
As with the Riemann zeta function, an element F of S has trivial zeroes that arise from the poles of the gamma factor γ(s). The other zeroes are referred to as the non-trivial zeroes of F. These will all be located in some strip 1 − A ≤ Re(s) ≤ A. Denoting the number of non-trivial zeroes of F with 0 ≤ Im(s) ≤ T by NF(T),[5] Selberg showed that
Here, dF is called the degree (or dimension) of F. It is given by[6]
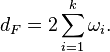 It can be shown that F = 1 is the only function in S whose degree is less than 1.
It can be shown that F = 1 is the only function in S whose degree is less than 1.
If F and G are in the Selberg class, then so is their product and
A function F ≠ 1 in S is called primitive if whenever it is written as F = F1F2, with Fi in S, then F = F1 or F = F2. If dF = 1, then F is primitive. Every function F ≠ 1 of S can be written as a product of primitive functions. Selberg's conjectures, described below, imply that the factorization into primitive functions is unique.
Examples of primitive functions include the Riemann zeta function and Dirichlet L-functions of primitive Dirichlet characters. Assuming conjectures 1 and 2 below, L-functions of irreducible cuspidal automorphic representations that satisfy the Ramanujan conjecture are primitive.[7]
Selberg's conjectures
In (Selberg 1992), Selberg made conjectures concerning the functions in S:
- Conjecture 1: For all F in S, there is an integer nF such that
- and nF = 1 whenever F is primitive.
- Conjecture 2: For distinct primitive F, F′ ∈ S,
- Conjecture 3: If
- is a factorization of F into primitive functions and χ is a primitive Dirichlet character, then
- and the Fiχ are primitive.
- Riemann hypothesis for S: For all F in S, the non-trivial zeroes of F all lie on the line Re(s) = 1/2.
Consequences of the conjectures
Conjectures 1 and 2 imply that if F has a pole of order m at s = 1, then F(s)/ζ(s)m is entire. In particular, they imply Dedekind's conjecture.[8]
M. Ram Murty showed in (Murty 1994) that conjectures 1 and 2 imply the Artin conjecture. In fact, Murty showed that Artin L-functions corresponding to irreducible representations of the Galois group of a solvable extension of the rationals are automorphic as predicted by the Langlands conjectures.[9]
The functions in S also satisfy an analogue of the prime number theorem: F(s) has no zeroes on the line Re(s) = 1. As mentioned above, conjectures 1 and 2 imply the unique factorization of functions in S into primitive functions. Another consequence is that the primitivity of F is equivalent to nF = 1.[10]
See also
Notes
- ↑ Conrey & Ghosh 1993, §1
- ↑ Lapidus, Michel Laurent (2008). In Search of the Riemann Zeros: Strings, Fractal Membranes and Noncommutative Spacetimes. American Mathematical Society. p. 389. ISBN 0821842226. Zbl 1150.11003.
- ↑ Murty 2008
- ↑ Murty 1994
- ↑ The zeroes on the boundary are counted with half-multiplicity.
- ↑ While the ωi are not uniquely defined by F, Selberg's result shows that their sum is well-defined.
- ↑ Murty 1994, Lemma 4.2
- ↑ A celebrated conjecture of Dedekind asserts that for any finite algebraic extension
 of
of  , the zeta function
, the zeta function 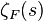 is divisible by the Riemann zeta function
is divisible by the Riemann zeta function  . That
is, the quotient
. That
is, the quotient  is entire. More generally, Dedekind conjectures that if
is entire. More generally, Dedekind conjectures that if
 is a finite extension of
is a finite extension of  , then
, then 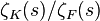 should be entire. This conjecture is
still open.
should be entire. This conjecture is
still open. - ↑ Murty 1994, Theorem 4.3
- ↑ Conrey & Ghosh 1993, § 4
References
- Selberg, Atle (1992), "Old and new conjectures and results about a class of Dirichlet series", Proceedings of the Amalfi Conference on Analytic Number Theory (Maiori, 1989), Salerno: Univ. Salerno, pp. 367–385, MR 1220477, Zbl 0787.11037 Reprinted in Collected Papers, vol 2, Springer-Verlag, Berlin (1991)
- Conrey, J. Brian; Ghosh, Amit (1993), "On the Selberg class of Dirichlet series: small degrees", Duke Mathematical Journal 72 (3): 673–693, arXiv:math.NT/9204217, MR 1253620, Zbl 0796.11037
- Murty, M. Ram (1994), "Selberg's conjectures and Artin L-functions", Bulletin of the American Mathematical Society, New Series (American Mathematical Society) 31 (1): 1–14, arXiv:math/9407219, MR 1242382, Zbl 0805.11062
- Murty, M. Ram (2008), Problems in analytic number theory, Graduate Texts in Mathematics, Readings in Mathematics 206 (Second ed.), Springer-Verlag, Chapter 8, doi:10.1007/978-0-387-72350-1, ISBN 978-0-387-72349-5, MR 2376618, Zbl 1190.11001
- Ivić, Aleksandar (2013), The theory of Hardy's Z-function, Cambridge Tracts in Mathematics 196, Cambridge: Cambridge University Press, ISBN 978-1-107-02883-8, Zbl pre06093527
| ||||||||||||||||||||