Seismic noise
In geology and other related disciplines, seismic noise is a generic name for a relatively persistent vibration of the ground, due to a multitude of causes, that is a non-interpretable or unwanted component of signals recorded by seismometers.
Physically, seismic noise consists mostly of surface waves. Low frequency waves (below 1 Hz) are generally called microseisms; high frequency waves (above 1 Hz) are called microtremors. Its causes include nearby human activities (such as traffic or heavy machinery), winds and other atmospheric phenomena, and ocean waves.
Seismic noise is relevant to any discipline that depends on seismology, such as geology, oil exploration, hydrology, and earthquake engineering, and structural health monitoring. It is often called ambient wavefield or ambient vibrations in those disciplines. (However, the latter term may also refer to vibrations transmitted through by air, building, or supporting structures.)
Seismic noise is a nuisance for activities that are sensitive to vibrations, such as accurate measurements, precision milling, telescopes, and crystal growing. On the other hand, seismic noise does have some practical uses, for example to determine the low-strain dynamic properties of civil-engineering structures, such as bridges, buildings, and dams; or to determine the elastic properties of the soil and subsoil in order to draw seismic microzonation maps showing the predicted ground response to earthquakes.
Causes
Research on the origin of seismic noise[1] indicates that the low frequency part of the spectrum (below 1 Hz) is due to natural causes, chiefly ocean waves. In particular the peak between 0.1 and 0.3 Hz is clearly associated with the interaction of water waves of nearly equal frequencies but opposite directions.[2][3][4][5] At high frequency (above 1 Hz), seismic noise is mainly produced by human activities such as road traffic and industrial work; but there are also natural sources, like rivers. Around 1 Hz, wind and other atmospheric phenomena are also a major source of ground vibrations.
Physical characteristics
The amplitude of seismic noise vibrations is typically in the order of 0.1 to 10 μm/s. High and low noise models as a function of frequency have been proposed.[6]
The seismic noise includes a small amount of body waves (P- and S-waves), but surface waves (Love and Rayleigh waves) predominate. Theses waves are dispersive, meaning that their phase velocity varies with frequency (most generally, it decreases with increasing frequency). Since the dispersion curve (phase velocity or slowness as a function of frequency) is tightly related to the variations of the shear-wave velocity with depth in the different ground layers, it can be used as a non-invasive tool to investigate the underground structure.
History
Seismic noise has very low amplitude and cannot be felt by humans. Their amplitude was also too low to be recorded by the first seismometers at the end of 19th century. However, at that time, the famous Japanese seismologist Fusakichi Omori could already record ambient vibrations in buildings, where the amplitudes are magnified. He found their resonance frequencies and studied their evolution as a function of damage.[7]
Applications to civil engineering
After the 1933 Long Beach earthquake in California, a large experiment campaign led by D. S. Carder [8] in 1935 allowed to record and analyze ambient vibrations in more than 200 buildings. These data were used in the design codes to estimate resonance frequencies of buildings but the interest of the method went down until the 1950s. Interest on ambient vibrations in structures grew further, especially in California and Japan, thanks to the work of earthquake engineers, including G. Housner, D. Hudson, K. Kanai, T. Tanaka, and others.[9]
Ambient vibrations were however supplanted - at least for some time - by forced vibration techniques that allow to increase the amplitudes and control the shaking source and their system identification methods. Even though M. Trifunac showed in 1972 that ambient and forced vibrations led to the same results,[10] the interest in ambient vibration techniques only rose in the late 1990s. They have now become quite attractive, due to their relatively low cost and convenience, and to the recent improvements in recording equipment and computation methods. The results of their low-strain dynamic probing were shown to be close enough to the dynamic characteristics measured under strong shaking, at least as long as the buildings are not severely damages.[11]
Scientific study and applications in geology
The recording of seismic noise directly from the ground started in the 1950s with the enhancement of seismometers to monitor nuclear tests and the development of seismic arrays. The main contributions at that time for the analysis of these recordings came from the Japanese seismologist K. Aki [12] in 1957. He proposed several methods used today for local seismic evaluation, such as Spatial Autocorrelation (SPAC), Frequency-wavenumber (FK), and correlation. However, the practical implementation of these methods was not possible at that time because of the low precision of clocks in seismic stations.
Again, improvements in instrumentation and algorithms led to renewed interest on those methods in the 1990s. Y.Nakamura rediscovered in 1989 the Horizontal to Vertical Spectral Ratio (H/V) method to derive the resonance frequency of sites.[13] Assuming that shear waves dominate the microtremor, Nakamura observed that the H/V spectral ratio of ambient vibrations was roughly equal to the S-wave transfer function between the ground surface and the bedrock at a site. (However, this assumption has been questioned by the SESAME project.)
In the late 1990s, array methods applied to seismic noise data started to yield ground properties in terms of shear waves velocity profiles.[14][15][16][17] The European Research project SESAME [18] (2004–2006) worked to standardize the use of seismic noise to estimate the amplification of earthquakes by local ground characteristics.
Current use of ambient vibrations
Characterization of the ground properties
The analysis of the ambient vibrations leads to different products used to characterize the ground properties. From the easiest to the most complicated, these products are: power spectra, H/V peak, dispersion curves and autocorrelation functions.
Single-station methods:
- Computation of power spectra, e.g. Passive seismic.
- HVSR (H/V spectral ratio): The H/V technique is especially related to ambient vibration recordings. Bonnefoy-Claudet et al.[19] showed that peaks in the horizontal to vertical spectral ratios can be linked to the Rayleigh ellipticity peak, the Airy phase of the Love waves and/or the SH resonance frequencies depending on the proportion of these different types of waves in the ambient noise. By chance, all these values give however approximately the same value for a given ground so that H/V peak is a reliable method to estimate the resonance frequency of the sites. For 1 sediment layer on the bedrock, this value f0 is related to the velocity of S-waves Vs and the depth of the sediments H following:
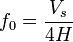 . It can therefore be used to map the bedrock depth knowing the S-wave velocity. This frequency peak allows to constrain the possible models obtain using other seismic methods but is not enough to derive a complete ground model. Moreover, it has been shown [20] that the amplitude of the H/V peak was not related to the magnitude of the amplification.
. It can therefore be used to map the bedrock depth knowing the S-wave velocity. This frequency peak allows to constrain the possible models obtain using other seismic methods but is not enough to derive a complete ground model. Moreover, it has been shown [20] that the amplitude of the H/V peak was not related to the magnitude of the amplification.
Array methods: Using an array of seismic sensors recording simultaneously the ambient vibrations allow to understand more deeply the wavefield and therefore to derive more properties of the ground. Due to the limitation of the available number of sensors, several arrays of different sizes may be realized and the results merged. The information of the Vertical components is only linked to the Rayleigh waves, and therefore easier to interpret, but method using the 3 space components are also developed, providing informations about Rayleigh and Love wavefield.
- FK, HRFK using the Beamforming technique
- SPAC (Spatial Auto-correlation) method
- Correlations methods
- Refraction microtremor ReMI
Characterization of the vibration properties of civil engineering structures
Like earthquakes, ambient vibrations force into vibrations the civil engineering structures like bridges, buildings or dams. This vibration source is supposed by the greatest part of the used methods to be a white noise, i.e. with a flat noise spectrum so that the recorded system response is actually characteristic of the system itself. The vibrations are perceptible by humans only in rare cases (bridges, high buildings). Ambient vibrations of buildings are also caused by wind and internal sources (machines, pedestrians...) but these sources are generally not used to characterize structures. The branch that studies the modal properties of systems under ambient vibrations is called Operational modal analysis (OMA) or Output-only modal analysis and provides many useful methods for civil engineering. The observed vibration properties of structures integrate all the complexity of these structures including the load-bearing system, heavy and stiff non-structural elements (infill masonry panels...), light non-structural elements (windows...) [21] and the interaction with the soil (the building foundation may not be perfectly fixed on the ground and differential motions may happen).[22] This is emphasized because it is difficult to produce models able to be compared with these measurements.
Single-station methods: The power spectrum computation of ambient vibration recordings in a structure (e.g. at the top floor of a building for larger amplitudes) gives an estimation of its resonance frequencies and eventually its damping ratio.
Transfer function method: Assuming ground ambient vibrations is the excitation source of a structure, for instance a building, the Transfer Function between the bottom and the top allows to remove the effects of a non-white input. This may particularly be useful for low signal-to-noise ratio signals (small building/high level of ground vibrations). However this method generally is not able to remove the effect of soil-structure interaction.[22]
Arrays: They consist in the simultaneous recording in several points of a structure. The objective is to obtain the modal parameters of structures: resonance frequencies, damping ratios and modal shapes for the whole structure. Notice than without knowing the input loading, the participation factors of these modes cannot a priori be retrieved. Using a common reference sensor, results for different arrays can be merged.
- Methods based on correlations
Several methods use the power spectral density matrices of simultaneous recordings, i.e. the cross-correlation matrices of these recordings in the Fourier domain. They allow to extract the operational modal parameters (Peak Picking method) that can be the results of modes coupling or the system modal parameters (Frequency Domain Decomposition method).
- System identification methods
Numerous system identification methods exist in the literature to extract the system properties and can be applied to ambient vibrations in structures
Inversion/Model updating/multi-model approach
The obtained results cannot directly give information on the physical parameters (S-wave velocity, structural stiffness...) of the ground structures or civil engineering structures. Therefore models are needed to compute these products (dispersion curve, modal shapes...) that could be compared with the experimental data. Computing a lot of models to find which agree with the data is solving the Inverse problem. The main issue of inversion is to well explore the parameter space with a limited number of computations of the model. However, the model fitting best the data is not the most interesting because parameter compensation, uncertainties on both models and data make many models with different input parameters as good compared to the data. The sensitivity of the parameters may also be very different depending on the model used. The inversion process is generally the weak point of these ambient vibration methods.
Material needed
The acquisition chain is mainly made of a seismic sensor and a digitizer. The number of seismic stations depends on the method, from single point (spectrum, HVSR) to arrays (3 sensors and more). Three components (3C) sensors are used except in particular applications. The sensor sensitivity and corner frequency depend also on the application. For ground measurements, velocimeters are necessary since the amplitudes are generally lower than the accelerometers sensitivity, especially at low frequency. Their corner frequency depends on the frequency range of interest but corner frequencies lower than 0.2 Hz are generally used. Geophones (generally 4.5 Hz corner frequency or greater) are generally not suited. For measurements in civil engineering structures, the amplitude is generally higher as well as the frequencies of interest, allowing the use of accelerometers or velocimeters with a higher corner frequency. However, since recording points on the ground may also be of interest in such experiments, sensitive instruments may be needed. Except for single station measurements, a common time stamping is necessary for all the stations. This can be achieved by GPS clock, common start signal using a remote control or the use of a single digitizer allowing the recording of several sensors. The relative location of the recording points is needed more or less precisely for the different techniques, requiring either manual distance measurements or differential GPS location.
Advantages and limitations
The advantages of ambient vibration techniques compared to active techniques commonly used in exploration geophysics or earthquake recordings used in Seismic tomography.
- Relatively cheap, non-invasive and non-destructive method
- Applicable to urban environment
- Provide valuable information with little data (e.g. HVSR)
- Dispersion curve of Rayleigh wave relatively easy to retrieve
- Provide reliable estimates of Vs30
Limitations of these methods are linked to the noise wavefield but especially to common assumptions made in seismic:
- Penetration depth depends on the array size but also on the noise quality, resolution and aliasing limits depend on the array geometry
- Complexity of the wavefield (Rayleigh, Love waves, interpretation of higher modes...)
- Plane wave assumption for most of the array methods (problem of sources within the array)
- 1D assumption of the underground structure, even though 2D was also undertaken [23]
- Inverse problem difficult to solve as for many geophysical methods
References
- ↑ S. Bonnefoy-Claudet, F. Cotton, and P.-Y. Bard (2006), The nature of noise wavefield and its applications for site effects studies. A literature review. Earth Science Review, volume 79, pages 205–227.
- ↑ M. S. Longuet-Higgins (1950). A theory of the origin of microseisms. Philosophical Transactions of the Royal Society of London, Series A, volume 243, pages 1–35.
- ↑ K. Hasselmann (1963), A statistical analysis of the generation of micro-seisms. Review of Geophysics, volume 1, issue 2, pages 177–210.
- ↑ S. Kedar, M. Longuet-Higgins, F. W. N. Graham, R. Clayton, and C. Jones (2008). The origin of deep ocean microseisms in the north Atlantic ocean. Proceedings of the Royal Society of London, series A, pages 1–35.
- ↑ F. Ardhuin, E. Stutzmann, M. Schimmel, and A. Mangeney (2011), Ocean wave sources of seismic noise. Journal of Geophysics Research, volume 115.
- ↑ Peterson (1993), Observation and modeling of seismic background noise. U.S. Geological Survey Technical Report 93-322, pages 1–95.
- ↑ C. Davison. Fusakichi Omori and his work on earthquakes. Bulletin of the Seismological Society of America, 14(4):240–255, 1924.
- ↑ D. S. Carder. Earthquake investigations in California, 1934-1935, chapter 5 Vibration observations, pages 49–106. Number Spec. Publ. n201. U.S. Coast and Geodetic Survey, 1936.
- ↑ Kanai, K., Tanaka, T., 1961. On microtremors VIII. Bulletin of the Earthquake Research Institute 39, 97–114
- ↑ M. Trifunac. Comparison between ambient and forced vibration experiments. Earthquake Engineering and Structural Dynamics, 1:133–150, 1972.
- ↑ Dunand, F., P. Gueguen, P.–Y. Bard, J. Rodgers and M. Celebi, 2006. Comparison Of The Dynamic Parameters Extracted From Weak, Moderate And Strong Motion Recorded In Buildings. First European Conference on Earthquake Engineering and Seismology (a joint event of the 13th ECEE & 30th General Assembly of the ESC) Geneva, Switzerland, 3–8 September 2006, Paper #1021
- ↑ Aki, K. (1957). Space and time spectra of stationary stochastic waves, with special reference to microtremors, Bull. Earthquake Res. Inst. 35, 415–457.
- ↑ Nakamura A Method for Dynamic Characteristic Estimation of SubSurface using Microtremor on the Ground Surface. Q Rep Railway Tech Res Inst 1989;30(1):25–33.
- ↑ Matshushima, T., and H. Okada, 1990. Determination of deep geological structures under urban areas using long-period microtremors, BUTSURI-TANSA, 43-1, p. 21-33.
- ↑ Milana, G., S. Barba, E. Del Pezzo, and E. Zambonelli, 1996. Site response from ambient noise measurements: new perspectives from an array study in Central Italy, Bull. seism. Soc. Am., 86-2, 320-328.
- ↑ Tokimatsu, K. , H. Arai, and Y. Asaka, 1996. Three-dimensional soil profiling in Kobé area using miccrotremors, Xth World Conf. Earthq. Engng., Acapulco, # 1486, Elsevier Science Ltd.
- ↑ Chouet, B., G. De Luca, G. Milana, P. Dawson, M. Martini and R. Scarpa, 1998. Shallow velocity structure of Stromboli Volcano, Italy, derived from small-aperture array measurements of strombolian tremor, Bull. seism. Soc. Am., 88-3, 653-666.
- ↑
- ↑ Bonnefoy-Claudet, S., C. Cornou, P.-Y. Bard, F. Cotton, P. Moczo, J. Kristek and D. Fäh, 2006. H/V ratio: a tool for site effects evaluation. Results from 1D noise simulations. Geophys. J. Int, 167, 827-837.
- ↑ Haghshenas, E., P.-Y. Bard, N. Theodulidis and SESAME WP04 Team, 2008. Empirical evaluation of microtremor H/V spectral ratio, Bulletin of Earthquake Engineering, 6-1, pp. 75-108, Feb. 2008.
- ↑ Hans S, Boutin C, Ibraim E, Roussillon P. In situ experiments and seismic analysis of existing buildings—Part I: experimental investigations. Earthquake Engineering and Structural Dynamics 2005; 34(12):1513–1529
- ↑ 22.0 22.1 M.I. Todorovska, “Seismic interferometry of a soil-structure interaction model with coupled horizontal and rocking response,” Bulletin of the Seismological Society of America, vol. 99, no. 2A, pp. 611–625, April 2009
- ↑ Roten, D.; Fäh, D. (2007). "A combined inversion of Rayleigh wave dispersion and 2-D resonance frequencies". Geophysical Journal International (Wiley) 168 (3): 1261–1275.