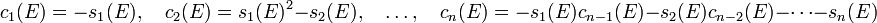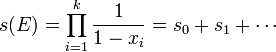Segre class

From Wikipedia, the free encyclopedia

In mathematics, the Segre class is a characteristic class used in the study of singular vector bundles. The total Segre class is inverse to the total Chern class, and thus provides equivalent information; the advantage of the Segre class is that it generalizes to singular vector bundles, while the Chern class does not. The Segre class is named after Beniamino Segre.

Definition

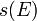For a holomorphic vector bundle $E$ over a complex manifold $M$ a total Segre class $s(E)$ is the inverse to the total Chern class 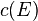$c(E)$ , see e.g.^[1]

Explicitly, for a total Chern class

$c(E)=1+c_{1}(E)+c_{2}(E)+\cdots \,$

one gets the total Segre class

$s(E)=1+s_{1}(E)+s_{2}(E)+\cdots \,$

where

$c_{1}(E)=-s_{1}(E),\quad c_{2}(E)=s_{1}(E)^{2}-s_{2}(E),\quad \dots ,\quad c_{n}(E)=-s_{1}(E)c_{{n-1}}(E)-s_{2}(E)c_{{n-2}}(E)-\cdots -s_{n}(E)$

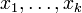Let $x_{1},\dots ,x_{k}$ be Chern roots, i.e. formal eigenvalues of ${\frac {i\Omega }{2\pi }}$ where $\Omega$ is a curvature of a connection on $E$ .

While the Chern class s(E) is written as

$c(E)=\prod _{{i=1}}^{{k}}(1+x_{i})=c_{0}+c_{1}+\cdots +c_{k}\,$

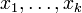
where $c_{i}$ is an elementary symmetric polynomial of degree $i$ in variables $x_{1},\dots ,x_{k}$

the Segre for the dual bundle $E^{\vee }$ which has Chern roots $-x_{1},\dots ,-x_{k}$ is written as

$s(E)=\prod _{{i=1}}^{{k}}{\frac {1}{1-x_{i}}}=s_{0}+s_{1}+\cdots$

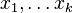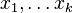
Expanding the above expression in powers of $x_{1},\dots x_{k}$ one can see that $s_{i}(E^{\vee })$ is represented by a complete homogeneous symmetric polynomial of $x_{1},\dots x_{k}$

References

↑ Fulton W. (1998). Intersection theory, p.50. Springer, 1998.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.