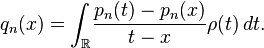Secondary polynomials
From Wikipedia, the free encyclopedia
In mathematics, the secondary polynomials 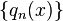 associated with a sequence
associated with a sequence  of polynomials orthogonal with respect to a density
of polynomials orthogonal with respect to a density 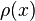 are defined by
are defined by
To see that the functions 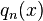 are indeed polynomials, consider the simple example of
are indeed polynomials, consider the simple example of 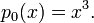 Then,
Then,
which is a polynomial  provided that the three integrals in
provided that the three integrals in 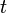 (the moments of the density
(the moments of the density  ) are convergent.
) are convergent.
See also
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.