Secant variety

From Wikipedia, the free encyclopedia

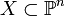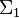In algebraic geometry, the Zariski closure of the union of the secant lines to a projective variety $X\subset {\mathbb {P}}^{n}$ is the first secant variety to $X$ . It is usually denoted $\Sigma _{1}$ .

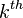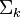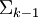The $k^{{th}}$ secant variety is the Zariski closure of the union of the linear spaces spanned by collections of k+1 points on $X$ . It is usually denoted $\Sigma _{k}$ . Unless $\Sigma _{k}={\mathbb {P}}^{n}$ , it is always singular along $\Sigma _{{k-1}}$ , but may have other singular points.

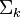If $X$ has dimension d, the dimension of $\Sigma _{k}$ is at most kd+d+k.

References

Joe Harris, Algebraic Geometry, A First Course, (1992) Springer-Verlag, New York. ISBN 0-387-97716-3

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.