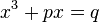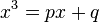Scipione del Ferro

From Wikipedia, the free encyclopedia

Scipione del Ferro
Born	6 February 1465
Died	5 November 1526(1526-11-05) (aged 61)
Residence	Bologna
Nationality	Bolognese (Italy)
Fields	Mathematics
Known for	Solution of the depressed cubic equation

Scipione del Ferro (6 February 1465 – 5 November 1526) was an Italian mathematician who first discovered a method to solve the depressed cubic equation.

Life

Scipione del Ferro was born in Bologna, in northern Italy, to Floriano and Filippa Ferro. His father, Floriano, worked in the paper industry, which owed its existence to the invention of the press in the 1450s and which probably allowed Scipione to access various works during early stages of his life. He married and had a daughter, who was named Filippa after his mother.

He likely studied at the University of Bologna, where he was appointed a lecturer in Arithmetic and Geometry in 1496. During his last years, he also undertook commercial work.

Diffusion of his work

There are no surviving scripts from del Ferro. This is in large part due to his resistance to communicating his works. Instead of publishing his ideas, he would only show them to a small, select group of friends and students.

It is suspected that this is due to the practice of mathematicians at the time of publicly challenging one another. When a mathematician accepted another's challenge, each mathematician needed to solve the other's problems. The loser in a challenge often lost funding or his university position. Del Ferro was fearful of being challenged and likely kept his greatest work secret so that he could use it to defend himself in the event of a challenge.

Despite this secrecy, he had a notebook where he recorded all his important discoveries. After his death in 1526, this notebook was inherited by his son-in-law Hannival Nave, who was married to del Ferro's daughter, Filippa. Nave was also a mathematician and a former student of del Ferro's, and he replaced del Ferro at the University of Bologna after his death.

In 1543, Gerolamo Cardano and Ludovico Ferrari (one of Cardano's students) travelled to Bologna to meet Nave and learn about his late father-in-law's notebook, where the solution to the depressed cubic equation appeared.

The Solution of the Cubic Equation

Mathematicians from del Ferro's time knew that the general cubic equation could be simplified to one of two cases called the depressed cubic equation, for positive numbers $p$ , $q$ , $x$ :

$x^{3}+px=q\,$

$x^{3}=px+q\,$

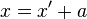The term in $x^{2}$ can always be removed by letting $x=x'+a$ for an appropriate constant $a$ .

While it is not known today with certainty the method that del Ferro used, it is thought that he used the fact that 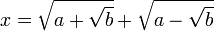$x={\sqrt {a+{\sqrt {b}}}}+{\sqrt {a-{\sqrt {b}}}}$ solves the equation $x^{2}=(2{\sqrt {a^{2}-b}})x^{0}+2a$ to conjecture that $x={\sqrt[ {3}]{a+{\sqrt {b}}}}+{\sqrt[ {3}]{a-{\sqrt {b}}}}$ solves $x^{3}=(3{\sqrt[ {3}]{a^{2}-b}})x+2a$ . This turns out to be true.

Then with the appropriate substitution of parameters, one can derive a solution to the depressed cubic: ${\sqrt[ {3}]{{\frac {q}{2}}+{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}+{\sqrt[ {3}]{{\frac {q}{2}}-{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}$

There are conjectures about whether del Ferro worked on a solution to the cubic equation as a result of Luca Pacioli's short tenure at the University of Bologna from 1501-1502. Pacioli had previously declared in Summa de arithmetica that he believed a solution to the equation to be impossible, fueling wide interest in the mathematical community.

It is unknown whether Scipione del Ferro solved both cases or not. However, in 1925, manuscripts were discovered by Bartolotti which contained del Ferro's method and made Bartolotti suspect that del Ferro had solved both cases.

Cardano, in his book Ars Magna (published in 1545) states that it was del Ferro who was the first to solve the cubic equation, and that the solution he gives is del Ferro's method.

Other contributions

Del Ferro also made other important contributions to the rationalization of fractions with denominators containing sums of cube roots.

He also investigated geometry problems with a compass set at a fixed angle, but little is known about his work in this area.

References

O'Connor, John; Robertson, Edmund (1999). "MacTutor History of Mathematics". University of St. Andrews.
Notable Mathematicians, Online Edition. Gale Group.
Cardano, Girolana (1545). Ars Magna.
Masotti, Arnaldo. Dictionary of Scientific Biography. pp. 595–597.
Merino, Orlando (2006). A short history of complex numbers.
García Venturini, Alejandro. Matemáticos Que Hicieron Historia.
Stewart, Ian (2004). Galois Theory, Third Edition. Chapman & Hall/CRC Mathematics.

Persondata
Name	Ferro, Scipione Del
Alternative names
Short description	Italian mathematician
Date of birth	6 February 1465
Place of birth
Date of death	5 November 1526
Place of death

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.