Schwarz minimal surface

From Wikipedia, the free encyclopedia

In differential geometry, the Schwarz minimal surfaces are periodic minimal surfaces originally described by Hermann Schwarz.

In the 1880s Schwarz and his student E. R. Neovius described periodic minimal surfaces.[1][2] They were later named by Alan Schoen in his seminal report that described the gyroid and other triply periodic minimal surfaces.[3]

The surfaces were generated using symmetry arguments: given a solution to Plateau's problem for a polygon, reflections of the surface across the boundary lines also produce valid minimal surfaces that can be continuously joined to the original solution. If a minimal surface meets a plane at right angles, then the mirror image in the plane can also be joined to the surface. Hence given a suitable initial polygon inscribed in a unit cell periodic surfaces can be constructed.[4]

The Schwarz surfaces have topological genus 3, the minimal genus of triply periodic minimal surfaces.[5]

They have been considered as models for periodic nanostructures in block copolymers, electrostatic equipotential surfaces in crystals.,[6] and hypothetical negatively curved graphite phases.[7]

Schwarz P ("Primitive")

Schwarz P surface

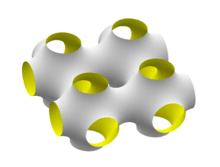
Schoen named this surface 'primitive' because it has two interwined congruent labyrinths, each with the shape of an inflated tubular version of the simple cubic lattice. While the standard P surface has cubic symmetry the unit cell can be any rectangular box, producing a family of minimal surfaces with the same topology.[8]

It can be approximated by the implicit surface

\cos(x)+\cos(y)+\cos(z)=0\ .[9]

The P surface has been considered for prototyping tissue scaffolds with a high surface-to-volume ratio and porosity.[10]

Schwarz D ("Diamond")

Schwarz D surface

Schoen named this surface 'diamond' because has two intertwined congruent labyrinths, each having the shape of an inflated tubular version of the diamond bond structure. It is sometimes called the F surface in the literature.

It can be approximated by the implicit surface

\sin(x)\sin(y)\sin(z)+\sin(x)\cos(y)\cos(z)+\cos(x)\sin(y)\cos(z)+\cos(x)\cos(y)\sin(z)=0.\

An exact expression exists in terms of elliptic integrals, based on the Weierstrass representation.[11]

Schwarz H ("Hexagonal")

Schwarz H surface

The H surface is similar to a catenoid with a triangular boundary, allowing it to tile space.

Schwarz CLP ("Crossed layers of parallels")

Schwarz CLP surface

Illustrations

References

  1. ↑ H. A. Schwarz, Gesammelte Mathematische Abhandlungen, Springer, Berlin, 1933.
  2. ↑ E. R. Neovius, "Bestimmung zweier spezieller periodischer Minimal achen", Akad. Abhandlungen, Helsingfors, 1883.
  3. ↑ Alan H. Schoen, Infinite periodic minimal surfaces without self-intersections, NASA Technical Note TN D-5541 (1970)
  4. ↑ Hermann Karcher, Konrad Polthier, "Construction of Triply Periodic Minimal Surfaces", Phil. Trans. R. Soc. Lond. A 16 September 1996 vol. 354 no. 1715 2077–2104
  5. ↑ http://schoengeometry.com/e_tpms.html
  6. ↑ Alan L. Mackay, "Periodic minimal surfaces", Physica B+C, Volume 131, Issues 1–3, August 1985, Pages 300–305
  7. ↑ H. Terrones and A. L. Mackay, "Negatively curved graphite and triply periodic minimal surfaces", Journal of Mathematical Chemistry, Volume 15, Number 1 (1994), 183–195, DOI:10.1007/BF01277558
  8. ↑ W. H. Meeks. The theory of triply-periodic minimal surfaces. Indiana University Math. Journal, 39 (3):877{936, 1990.
  9. ↑ http://archive.msri.org/about/sgp/jim/geom/level/library/triper/index.html
  10. ↑ Jaemin Shin, Sungki Kim, Darae Jeong, Hyun Geun Lee, Dongsun Lee, Joong Yeon Lim, and Junseok Kim, Finite Element Analysis of Schwarz P Surface Pore Geometries for Tissue-Engineered Scaffolds, Mathematical Problems in Engineering, Volume 2012, Article ID 694194, doi:10.1155/2012/694194
  11. ↑ Paul J.F. Gandy, Djurdje Cvijović, Alan L. Mackay, Jacek Klinowski, Exact computation of the triply periodic D (`diamond') minimal surface, Chemical Physics Letters, Volume 314, Issues 5–6, 10 December 1999, Pages 543–551
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.