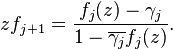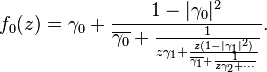Schur class

From Wikipedia, the free encyclopedia

In mathematics, the Schur class consists of the Schur functions: the holomorphic functions from the open unit disk to the closed unit disk. These functions were studied by Schur (1918).

The Schur parameters γ_j of a Schur function f₀ are defined recursively by

$\gamma _{j}=f_{j}(0)$

$zf_{{j+1}}={\frac {f_{j}(z)-\gamma _{j}}{1-\overline {\gamma _{j}}f_{j}(z)}}.$

The Schur parameters γ_j all have absolute value at most 1.

This gives a continued fraction expansion of the Schur function f₀ by repeatedly using the fact that

$f_{j}(z)=\gamma _{j}+{\frac {1-|\gamma _{j}|^{2}}{\overline {\gamma _{j}}+{\frac {1}{zf_{{j+1}}(z)}}}}$

which gives

$f_{0}(z)=\gamma _{0}+{\frac {1-|\gamma _{0}|^{2}}{\overline {\gamma _{0}}+{\frac {1}{z\gamma _{1}+{\frac {z(1-|\gamma _{1}|^{2})}{\overline {\gamma _{1}}+{\frac {1}{z\gamma _{2}+\cdots }}}}}}}}.$

References

Schur, I. (1918), "Über Potenzreihen, die im Innern des Einheitskreises beschränkt sind. I, II", J. Reine Angew. Math. (in German) (Berlin: Walter de Gruyter) 147,: 205–232, doi:10.1515/crll.1917.147.205, Zbl 46.0475.01
Simon, Barry (2005), Orthogonal polynomials on the unit circle. Part 1. Classical theory, American Mathematical Society Colloquium Publications 54, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-3446-6, MR 2105088
Simon, Barry (2005), Orthogonal polynomials on the unit circle. Part 2. Spectral theory, American Mathematical Society Colloquium Publications 54, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-3675-0, MR 2105089

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.