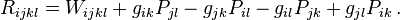Schouten tensor

From Wikipedia, the free encyclopedia

In Riemannian geometry, the Schouten tensor is a second-order tensor introduced by Jan Arnoldus Schouten. It is defined by, for n ≥ 3,

P={\frac {1}{n-2}}\left(Ric-{\frac {R}{2(n-1)}}g\right)\,\Leftrightarrow Ric=(n-2)P+Jg\,,

where Ric is the Ricci tensor, R is the scalar curvature, g is the Riemannian metric, J={\frac {1}{2(n-1)}}R is the trace of P and n is the dimension of the manifold.

The Weyl tensor equals the Riemann curvature tensor minus the Kulkarni–Nomizu product of the Schouten tensor with the metric. In an index notation

R_{{ijkl}}=W_{{ijkl}}+g_{{ik}}P_{{jl}}-g_{{jk}}P_{{il}}-g_{{il}}P_{{jk}}+g_{{jl}}P_{{ik}}\,.

The Schouten tensor often appears in conformal geometry because of its relatively simple conformal transformation law

g_{{ij}}\mapsto \Omega ^{2}g_{{ij}}\Rightarrow P_{{ij}}\mapsto P_{{ij}}-\nabla _{i}\Upsilon _{j}+\Upsilon _{i}\Upsilon _{j}-{\frac 12}\Upsilon _{k}\Upsilon ^{k}g_{{ij}}\,,

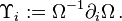
where \Upsilon _{i}:=\Omega ^{{-1}}\partial _{i}\Omega \,.

Further reading

  • Arthur L. Besse, Einstein Manifolds. Springer-Verlag, 2007. See Ch.1 §J "Conformal Changes of Riemannian Metrics."
  • Spyros Alexakis, The Decomposition of Global Conformal Invariants. Princeton University Press, 2012. Ch.2, noting in a footnote that the Schouten tensor is a "trace-adjusted Ricci tensor" and may be considered as "essentially the Ricci tensor."
  • Wolfgang Kuhnel and Hans-Bert Rademacher, "Conformal diffeomorphisms preserving the Ricci tensor", Proc. Amer. Math. Soc. 123 (1995), no. 9, 2841–2848. Online eprint (pdf).
  • T. Bailey, M.G. Eastwood and A.R. Gover, "Thomas's Structure Bundle for Conformal, Projective and Related Structures", Rocky Mountain Journal of Mathematics, vol. 24, Number 4, 1191-1217.

See also


This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.