Schlegel diagram

From Wikipedia, the free encyclopedia
Examples colored by the number of sides on each face. Yellow triangles, red squares, and green pentagons.
A tesseract projected into 3-space as a Schlegel diagram. There are 8 cubic cells visible, one in the center, one below each of the six exterior faces, and the last one is inside-out representing the space outside the cubic boundary.

In geometry, a Schlegel diagram is a projection of a polytope from 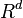R^{d} into R^{{d-1}} through a point beyond one of its facets. The resulting entity is a polytopal subdivision of the facet in R^{{d-1}} that is combinatorially equivalent to the original polytope. In 1886 Victor Schlegel introduced this tool for studying combinatorial and topological properties of polytopes. In dimensions 3 and 4, a Schlegel diagram is a projection of a polyhedron into a plane figure and a projection of a polychoron to 3-space, respectively. As such, Schlegel diagrams are commonly used as a means of visualizing four-dimensional polytopes.

Construction

A Schlegel diagram can be constructed by a perspective projection viewed from a point outside of the polytope, above the center of a facet. All vertices and edges of the polytope are projected onto a hyperplane of that facet. If the polytope is convex, a point near the facet will exist which maps the facet outside, and all other facets inside, so no edges need to cross in the projection.

Examples

Dodecahedron Dodecaplex

12 pentagon faces in the plane
120 dodecahedral cells in 3-space

See also

  • Net (polyhedron) – A different approach for visualization by lowering the dimension of a polytope is to build a net, disconnecting facets, and unfolding until the facets can exist on a single hyperplane. This maintains the geometric scale and shape, but makes the topological connections harder to see.

References

  • Victor Schlegel (1883) Theorie der homogen zusammengesetzten Raumgebilde, Nova Acta, Ksl. Leop.-Carol. Deutsche Akademie der Naturforscher, Band XLIV, Nr. 4, Druck von E. Blochmann & Sohn in Dresden.
  • Victor Schlegel (1886) Ueber Projectionsmodelle der regelmässigen vier-dimensionalen Körper, Waren.
  • Coxeter, H.S.M.; Regular Polytopes, (Methuen and Co., 1948). (p. 242)
  • Grünbaum, Branko (2003), Kaibel, Volker; Klee, Victor; Ziegler, Günter M., eds., Convex polytopes (2nd ed.), New York & London: Springer-Verlag, ISBN 0-387-00424-6 .

External links

Wikimedia Commons has media related to Schlegel diagrams.
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.