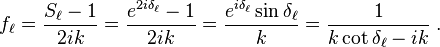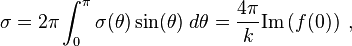Scattering amplitude

From Wikipedia, the free encyclopedia

In quantum physics, the scattering amplitude is the amplitude of the outgoing spherical wave relative to the incoming plane wave in a stationary-state scattering process.^[1] The latter is described by the wavefunction

$\psi ({\mathbf {r}})=e^{{ikz}}+f(\theta ){\frac {e^{{ikr}}}{r}}\;,$

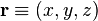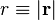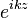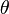where ${\mathbf {r}}\equiv (x,y,z)$ is the position vector; $r\equiv |{\mathbf {r}}|$ ; $e^{{ikz}}$ is the incoming plane wave with the wavenumber $k$ along the $z$ axis; $e^{{ikr}}/r$ is the outgoing spherical wave; $\theta$ is the scattering angle; and 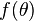$f(\theta )$ is the scattering amplitude. The dimension of the scattering amplitude is length.

The scattering amplitude is a probability amplitude and the differential cross-section as a function of scattering angle is given as its modulus squared

${\frac {d\sigma }{d\Omega }}=|f(\theta )|^{2}\;.$

In the low-energy regime the scattering amplitude is determined by the scattering length.

Partial wave expansion

In the partial wave expansion the scattering amplitude is represented as a sum over the partial waves,^[2]

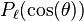$f(\theta )=\sum _{{\ell =0}}^{\infty }(2\ell +1)f_{\ell }(k)P_{\ell }(\cos(\theta ))\;,$

where $f_{\ell }(k)$ is the partial amplitude and $P_{\ell }(\cos(\theta ))$ is the Legendre polynomial.

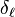The partial amplitude can be expressed via the S-matrix element $S_{\ell }=e^{{2i\delta _{\ell }}}$ and the scattering phase shift $\delta _{\ell }$ as

$f_{\ell }={\frac {S_{\ell }-1}{2ik}}={\frac {e^{{2i\delta _{\ell }}}-1}{2ik}}={\frac {e^{{i\delta _{\ell }}}\sin \delta _{\ell }}{k}}={\frac {1}{k\cot \delta _{\ell }-ik}}\;.$

Then the differential cross section is given by^[3]

$\sigma (\theta )=|f(\theta )|^{2}={\frac {1}{k^{2}}}\left|\sum _{{\ell =0}}^{\infty }(2\ell +1)e^{{i\delta _{\ell }}}\sin(\delta _{\ell })P_{\ell }(\cos(\theta ))\right|^{2}\;,$

and the total elastic cross section becomes

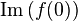$\sigma =2\pi \int _{0}^{\pi }\sigma (\theta )\sin(\theta )\;d\theta ={\frac {4\pi }{k}}{\text{Im}}\left(f(0)\right)\;,$

where ${\text{Im}}\left(f(0)\right)$ is the imaginary part of $f(0)$ .

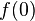X-rays

The scattering length for X-rays is the Thompson scattering length or classical electron radius, 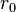$r_{0}$ .

Neutrons

The nuclear neutron scattering process involves the coherent neutron scattering length, often described by $b$ .

Quantum mechanical formalism

A quantum mechanical approach is given by the S matrix formalism.

References

↑ Quantum Mechanics: Concepts and Applications By Nouredine Zettili, 2nd edition, page 623. ISBN 978-0-470-02679-3 Paperback 688 pages January 2009, ©2008
↑ Michael Fowler/ 1/17/08 Plane Waves and Partial Waves
↑ Schiff, Leonard I. (1968). Quantum Mechanics. New York: McGraw Hill. pp. 119–120.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.