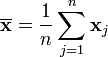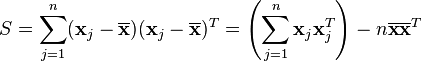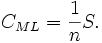Scatter matrix

From Wikipedia, the free encyclopedia
For the notion in quantum mechanics, see scattering matrix.

In multivariate statistics and probability theory, the scatter matrix is a statistic that is used to make estimates of the covariance matrix of the multivariate normal distribution.

Definition

Given n samples of m-dimensional data, represented as the m-by-n matrix, X=[{\mathbf {x}}_{1},{\mathbf {x}}_{2},\ldots ,{\mathbf {x}}_{n}], the sample mean is

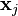\overline {{\mathbf {x}}}={\frac {1}{n}}\sum _{{j=1}}^{n}{\mathbf {x}}_{j}

where {\mathbf {x}}_{j} is the jth column of X\,.

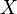The scatter matrix is the m-by-m positive semi-definite matrix

S=\sum _{{j=1}}^{n}({\mathbf {x}}_{j}-\overline {{\mathbf {x}}})({\mathbf {x}}_{j}-\overline {{\mathbf {x}}})^{T}=\left(\sum _{{j=1}}^{n}{\mathbf {x}}_{j}{\mathbf {x}}_{j}^{T}\right)-n\overline {{\mathbf {x}}}\overline {{\mathbf {x}}}^{T}

where T denotes matrix transpose. The scatter matrix may be expressed more succinctly as

S=X\,C_{n}\,X^{T}

where \,C_{n} is the n-by-n centering matrix.

Application

The maximum likelihood estimate, given n samples, for the covariance matrix of a multivariate normal distribution can be expressed as the normalized scatter matrix

C_{{ML}}={\frac {1}{n}}S.

When the columns of 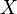X\, are independently sampled from a multivariate normal distribution, then S\, has a Wishart distribution.

See also


This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.