Sawtooth (cellular automaton)

The number of alive cells plotted versus the number of elapsed generations for the first sawtooth discovered

Example of a sawtooth pattern living through several drops below the maximum live cell count. Click on the image to see the cell pattern.

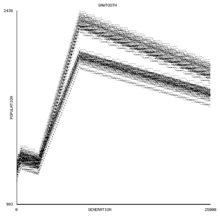
In a cellular automaton, a finite pattern is called a sawtooth if its population grows without bound but does not tend to infinity. In other words, a sawtooth is a pattern with population that reaches new heights infinitely often, but also infinitely often drops below some fixed value.^[1] Their name comes from the fact that their plot of population versus generation number looks roughly like an ever-increasing sawtooth wave.

The first sawtooth in Conway's Game of Life was constructed by Dean Hickerson in April 1991 by using a loaf tractor beam. The least infinitely repeating population of any known sawtooth is 262, which is attained by a sawtooth found by David Bell on July 9, 2005.^[2]

Expansion factor

The expansion factor of a sawtooth is the limit of the ratio of successive heights (or equivalently, widths) of the "teeth" in plots of population versus generation number. Some sawtooths do not have an expansion factor under its standard definition because some sawtooths have growth that is not exponentially-spaced.^[3]

References

1. ↑ "Life Lexicon "S"". Stephen Silver. February 28, 2006. Retrieved March 13, 2009. 
2. ↑ "New Sawtooth Patterns". Dave Greene. August 10, 2005. Retrieved March 13, 2009. 
3. ↑ "Parabolic sawtooth". Paul Callahan. Retrieved March 13, 2009. 

External links

• List of known sawtooths at LifeWiki