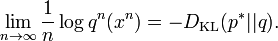Sanov's theorem

From Wikipedia, the free encyclopedia

In information theory, Sanov's theorem gives a bound on the probability of observing an atypical sequence of samples from a given probability distribution.

Let A be a set of probability distributions over an alphabet X, and let q be an arbitrary distribution over X (where q may or may not be in A). Suppose we draw n i.i.d. samples from q, represented by the vector $x^{n}=x_{1},x_{2},\ldots ,x_{n}$ . Further, let us ask that the empirical distribution, 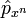${\hat {p}}_{{x^{n}}}$ , of the samples falls within the set A -- formally, we write $\{x^{n}:{\hat {p}}_{{x^{n}}}\in A\}$ . Then,

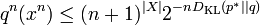$q^{n}(x^{n})\leq (n+1)^{{|X|}}2^{{-nD_{{{\mathrm {KL}}}}(p^{*}||q)}}$ ,

where

$q^{n}(x^{n})$ is shorthand for $q(x_{1})q(x_{2})\cdots q(x_{n})$ , and
$p^{*}$ is the information projection of q onto A.

In words, the probability of drawing an atypical distribution is proportional to the KL distance from the true distribution to the atypical one; in the case that we consider a set of possible atypical distributions, there is a dominant atypical distribution, given by the information projection.

Furthermore, if A is a closed set,

$\lim _{{n\to \infty }}{\frac {1}{n}}\log q^{n}(x^{n})=-D_{{{\mathrm {KL}}}}(p^{*}||q).$

References

Cover, Thomas M.; Thomas, Joy A. (2006). Elements of Information Theory (2 ed.). Hoboken, New Jersey: Wiley Interscience. p. 362.

Sanov, I. N. (1957) "On the probability of large deviations of random variables". Mat. Sbornik 42, 11–44.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.