S/KEY

From Wikipedia, the free encyclopedia

S/KEY is a one-time password system developed for authentication to Unix-like operating systems, especially from dumb terminals or untrusted public computers on which one does not want to type a long-term password. A user's real password is combined in an offline device with a short set of characters and a decrementing counter to form a single-use password. Because each password is only used once, they are useless to password sniffers.

Because the short set of characters does not change until the counter reaches zero, it is possible to prepare a list of single-use passwords, in order, that can be carried by the user. Alternatively, the user can present the password, characters, and desired counter value to a local calculator to generate the appropriate one-time password that can then be transmitted over the network in the clear. The latter form is more common and practically amounts to challenge-response authentication.

S/KEY is supported in Linux (via Pluggable authentication modules), OpenBSD, NetBSD, and FreeBSD, and a generic open source implementation can be used to enable its use on other systems. One common implementation is called OPIE. S/KEY is a trademark of Telcordia Technologies, formerly known as Bell Communications Research (Bellcore).

S/KEY is also sometimes referred to as Lamport's scheme, after its author, Leslie Lamport. It was developed by Neil Haller, Phil Karn and John Walden at Bellcore in the late 1980s. With the expiration of the basic patents on public key cryptography and the widespread use of laptop computers running SSH and other cryptographic protocols that can secure an entire session, not just the password, S/KEY is falling into disuse.^{[citation needed]} Schemes that implement two-factor authentication, by comparison, are growing in use.^[1]

Password generation

The server is the computer that will perform the authentication.

S/KEY password generation

This step begins with a secret key 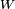$\scriptstyle W$ . This secret can either be provided by the user, or can be generated by a computer. Either way, if this secret is disclosed then the security of S/KEY is compromised
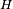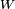A cryptographic hash function $\scriptstyle H$ is applied $\scriptstyle n$ times to $\scriptstyle W$ , thereby producing a hash chain of $\scriptstyle n$ one-time passwords. The passwords are the results of the application of the cryptographic hash function:
$H(W),H(H(W)),\dots ,H^{n}(W)\,$
The initial secret 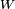$\scriptstyle W$ is discarded
The user is provided with the $\scriptstyle n$ passwords, printed out in reverse order: $\scriptstyle H^{n}(W),\,H^{{n-1}}(W),\,\dots ,\,H(H(W)),\,H(W)\,$
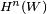The passwords $\scriptstyle H(W),\,H(H(W)),\,\dots ,\,H^{{n-1}}(W)\,$ are discarded from the server. Only the password $\scriptstyle \scriptstyle H^{n}(W)$ , the one at the top of the user's list, is stored on the server.

Authentication

S/KEY authentication

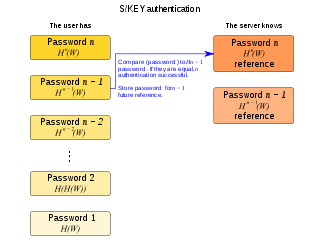
After password generation, the user has a sheet of paper with $\scriptstyle n$ passwords on it.

More ideally, though perhaps less commonly in practice, the user may carry a small, portable, secure, non-networked computing device capable of regenerating any needed password given the secret passphrase, the salt, and the number of iterations of the hash required, the latter two of which are conveniently provided by the server requesting authentication for login.

In any case, the first password will be the same password that the server has stored. This first password will not be used for authentication (the user should scratch this password on the sheet of paper), the second one will be used instead:

The user provides the server with the second password $\scriptstyle {\text{pwd}}$ on the list and scratches that password.
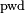The server attempts to compute $\scriptstyle H({\text{pwd}})$ where $\scriptstyle {\text{pwd}}$ is the password supplied. If $\scriptstyle H({\text{pwd}})$ produces the first password (the one the server has stored), then the authentication is successful. The server will then store $\scriptstyle {\text{pwd}}$ as the current reference.

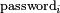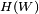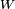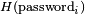For subsequent authentications, the user will provide $\scriptstyle {\text{password}}_{i}$ . (The last password on the printed list, password $\scriptstyle n$ , is the first password generated by the server, $\scriptstyle H(W)$ , where $\scriptstyle W$ is the initial secret). The server will compute $\scriptstyle H({\text{password}}_{i})$ and will compare the result to password 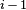$\scriptstyle i\,-\,1$ , which is stored as reference on the server.

Security

The security of S/KEY relies on the difficulty of reversing cryptographic hash functions. Assume an attacker manages to get hold of a password that was used for a successful authentication. Supposing this is password i, this password is already useless for subsequent authentications, because each password can only be used once. It would be interesting for the attacker to find out password i − 1, because this password is the one that will be used for the next authentication.

However this would require inverting the hash function that produced password i − 1 using password i (H(password i − 1) = password i), which is extremely difficult to do with current cryptographic hash functions.

S/KEY is however vulnerable to a man in the middle attack if used by itself. It is also vulnerable to certain race conditions, such as where an attacker's software sniffs the network to learn the first N-1 characters in the password (where N equals the password length), establishes its own TCP session to the server, and in rapid succession tries all valid characters in the Nth position until one succeeds. These types of vulnerabilities can be avoided by using ssh, SSL, SPKM, or other encrypted transport layer.

Since each iteration of S/KEY doesn't include the salt or count, it is feasible to find collisions directly without breaking the initial password. This has a complexity of 2⁶⁴, which can be pre-calculated with the same amount of space. The space complexity can be optimized by storing chains of values, although collisions might reduce the coverage of this method, especially for long chains.^[2]

Somebody with an S/KEY database in their hands can break all of them in parallel with a complexity of 2⁶⁴. While they wouldn't get the original password, they would be able to find valid credentials for each user. In this regard, it is similar to storing unsalted 64-bit hashes of strong, unique passwords.

The S/KEY protocol can loop. If such a loop were created in the S/KEY chain, an attacker could use your key without finding the original value, and possibly without tipping off the valid user. The pathological case of this would be an OTP which hashes to itself.

Usability

Internally, S/KEY uses 64 bit numbers. For human usability purposes, each number is mapped to six short words, of one to four characters each, from a publicly accessible 2048-word dictionary. For example, one 64 bit number maps to "ROY HURT SKI FAIL GRIM KNEE".^[3]

References

↑ "Global Two-factor Authentication Market 2010-2014". Infiniti Research Limited. 2011-09-22. Retrieved 2012-02-09.
↑ Samuel, Michael. "OTP Weaknesses".
↑ Haller, Neil; Metz, Craig; Nesser II, Philip J.; Straw, Mike. "Appendix D: Dictionary for Converting Between 6-Word and Binary Formats". A One-Time Password System. IETF.

External links

The S/KEY One-Time Password System (RFC 1760)
A One-Time Password System (RFC 2289)
jsotp: JavaScript OTP & S/Key Calculator
Introduction to the system
Java Micro Edition S/key calculator for cell phones

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.