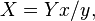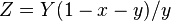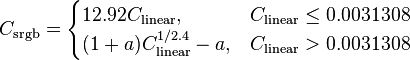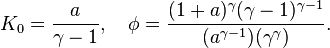SRGB

sRGB is a standard RGB color space created cooperatively by HP and Microsoft in 1996 for use on monitors, printers and the Internet.
sRGB uses the ITU-R BT.709 primaries, the same as are used in studio monitors and HDTV,[1] and a transfer function (gamma curve) typical of CRTs. This specification allowed sRGB to be directly displayed on typical CRT monitors of the time, a factor which greatly aided its acceptance.
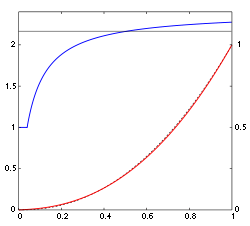
Unlike most other RGB color spaces, the sRGB gamma cannot be expressed as a single numerical value. The overall gamma is approximately 2.2, consisting of a linear (gamma 1.0) section near black, and a non-linear section elsewhere involving a 2.4 exponent and a gamma (slope of log output versus log input) changing from 1.0 through about 2.3.
Background
The sRGB color space has been endorsed by the W3C, Exif, Intel, Pantone, Corel, and many other industry players. It is used in proprietary and open graphics file formats, such as SVG.
The sRGB color space is well specified and is designed to match typical home and office viewing conditions, rather than the darker environment typically used for commercial color matching.
Much software is now designed with the assumption that an 8-bit-per-channel image file placed unchanged onto an 8-bit-per-channel display will appear much as the sRGB specification recommends. LCDs, digital cameras, printers, and scanners all follow the sRGB standard. Devices which do not naturally follow sRGB (like older CRT monitors did) include compensating circuitry or software so that, in the end, they also obey this standard. For this reason, one can generally assume, in the absence of embedded profiles or any other information, that any 8-bit-per-channel image file or any 8-bit-per-channel image API or device interface can be treated as being in the sRGB color space. However, when the correct displaying of an RGB color space is needed, color management usually must be employed.
The sRGB gamut
sRGB defines the chromaticities of the red, green, and blue primaries, the colors where one of the three channels is nonzero and the other two are zero. The gamut of chromaticities that can be represented in sRGB is the color triangle defined by these primaries. As with any RGB color space, for non-negative values of R, G, and B it is not possible to represent colors outside this triangle, which is well inside the range of colors visible to a human.
| Chromaticity | Red | Green | Blue | White point |
|---|---|---|---|---|
| x | 0.6400 | 0.3000 | 0.1500 | 0.3127 |
| y | 0.3300 | 0.6000 | 0.0600 | 0.3290 |
| Y | 0.2126 | 0.7153 | 0.0721 | 1.0000 |
sRGB also defines a nonlinear transformation between the intensity of these primaries and the actual number stored. The curve is similar to the gamma response of a CRT display. It is more important to replicate this curve than the primaries to get correct display of an sRGB image. This nonlinear conversion means that sRGB is a reasonably efficient use of the values in an integer-based image file to display human-discernible light levels.
sRGB is sometimes avoided by high-end print publishing professionals because its color gamut is not big enough, especially in the blue-green colors, to include all the colors that can be reproduced in CMYK printing.
Specification of the transformation
The forward transformation (CIE xyY or CIE XYZ to sRGB)
The first step in the calculation of sRGB tristimulus values from the CIE XYZ tristimulus values is a linear transformation, which may be carried out by a matrix multiplication. The numerical values below match those in the official sRGB specification (IEC 61966-2-1:1999) and differ slightly from those in a publication by sRGB's creators.[2] Note that these linear values are not the final result.
Note also, that if the CIE xyY color space values are given (where x, y are the chromaticity coordinates and Y is the luminance), they must first be transformed to CIE XYZ tristimulus values by:
The intermediate parameters  ,
, 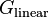 and
and  for in-gamut colors are defined to be in the range [0,1], which means that the initial X, Y, and Z values need to be similarly scaled (if you start with XYZ values going to 100 or so, divide them by 100 first, or apply the matrix and then scale by a constant factor to the [0,1] range). The linear RGB values are usually clipped to that range, with display white represented as (1,1,1); the corresponding original XYZ values are such that white is D65 with unit luminance (X,Y,Z = 0.9505, 1.0000, 1.0890). Calculations assume the 2° standard colorimetric observer.[2]
for in-gamut colors are defined to be in the range [0,1], which means that the initial X, Y, and Z values need to be similarly scaled (if you start with XYZ values going to 100 or so, divide them by 100 first, or apply the matrix and then scale by a constant factor to the [0,1] range). The linear RGB values are usually clipped to that range, with display white represented as (1,1,1); the corresponding original XYZ values are such that white is D65 with unit luminance (X,Y,Z = 0.9505, 1.0000, 1.0890). Calculations assume the 2° standard colorimetric observer.[2]
sRGB was designed to reflect a typical real-world monitor with a gamma of 2.2, and the following formula transforms the linear values into sRGB. Let  be
be  ,
, 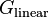 , or
, or  , and
, and 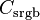 be
be  ,
, 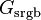 or
or  :
:
- where

These gamma-corrected values are in the range 0 to 1. If values in the range 0 to 255 are required, e.g. for video display or 8-bit graphics, the usual technique is to multiply by 255 and round to an integer.
The reverse transformation
Again the sRGB component values  ,
, 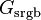 ,
,  are in the range 0 to 1. (A range of 0 to 255 can simply be divided by 255).
are in the range 0 to 1. (A range of 0 to 255 can simply be divided by 255).
(where  is
is  ,
,  , or
, or  ). Followed by a matrix multiplication of the linear values to get XYZ:
). Followed by a matrix multiplication of the linear values to get XYZ:
Theory of the transformation
It is often casually stated that the decoding gamma for sRGB data is 2.2, yet the above transform shows an exponent of 2.4. This is because the net effect of the piecewise decomposition is necessarily a changing instantaneous gamma at each point in the range: it goes from gamma = 1 at zero to a gamma of 2.4 at maximum intensity with a median value being close to 2.2. The transformation was designed to approximate a gamma of about 2.2, but with a linear portion near zero to avoid having an infinite slope at K = 0, which can cause numerical problems. The continuity condition for the curve  which is defined above as a piecewise function of
which is defined above as a piecewise function of 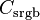 , is
, is
Solving with  and the standard value
and the standard value 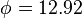 yields two solutions,
yields two solutions, 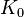 ≈
≈  or
or 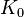 ≈
≈ 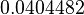 . The IEC 61966-2-1 standard uses the rounded value
. The IEC 61966-2-1 standard uses the rounded value  . However, if we impose the condition that the slopes match as well then we must have
. However, if we impose the condition that the slopes match as well then we must have
We now have two equations. If we take the two unknowns to be 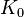 and
and  then we can solve to give
then we can solve to give
Substituting  and
and  gives
gives 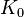 ≈
≈ 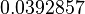 and
and  ≈
≈  , with the corresponding linear-domain threshold at
, with the corresponding linear-domain threshold at  ≈
≈  . These values, rounded to
. These values, rounded to  ,
, 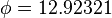 , and
, and 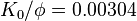 , are sometimes used to describe sRGB conversion.[3] Publications by sRGB's creators[2] rounded to
, are sometimes used to describe sRGB conversion.[3] Publications by sRGB's creators[2] rounded to  and
and 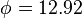 , resulting in a small discontinuity in the curve. Some authors adopted these values in spite of the discontinuity.[4] For the standard, the rounded value
, resulting in a small discontinuity in the curve. Some authors adopted these values in spite of the discontinuity.[4] For the standard, the rounded value 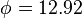 was kept and the
was kept and the 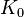 value was recomputed to make the resulting curve continuous, as described above, resulting in a slope discontinuity from 12.92 below the intersection to 12.70 above.
value was recomputed to make the resulting curve continuous, as described above, resulting in a slope discontinuity from 12.92 below the intersection to 12.70 above.
Viewing environment
| Parameter | Value |
|---|---|
| Luminance level | 80 cd/m2 |
| Illuminant white point | x = 0.3127, y = 0.3291 (D65) |
| Image surround reflectance | 20% (~medium gray) |
| Encoding ambient illuminance level | 64 lux |
| Encoding ambient white point | x = 0.3457, y = 0.3585 (D50) |
| Encoding viewing flare | 1.0% |
| Typical ambient illuminance level | 200 lux |
| Typical ambient white point | x = 0.3457, y = 0.3585 (D50) |
| Typical viewing flare | 5.0% |
The sRGB specification assumes a dimly lit encoding (creation) environment with an ambient correlated color temperature (CCT) of 5000 K. It is interesting to note that this differs from the CCT of the illuminant (D65). Using D50 for both would have made the white point of most photographic paper appear excessively blue.[5] The other parameters, such as the luminance level, are representative of a typical CRT monitor.
For optimal results, the ICC recommends using the encoding viewing environment (i.e., dim, diffuse lighting) rather than the less-stringent typical viewing environment.[2]
Usage
Due to the standardization of sRGB on the Internet, on computers, and on printers, many low- to medium-end consumer digital cameras and scanners use sRGB as the default (or only available) working color space. As the sRGB gamut meets or exceeds the gamut of a low-end inkjet printer, an sRGB image is often regarded as satisfactory for home use. However, consumer-level CCDs are typically uncalibrated, meaning that even though the image is being labeled as sRGB, one can't conclude that the image is color-accurate sRGB.
If the color space of an image is unknown and it is an 8- to 16-bit image format, assuming it is in the sRGB color space is a safe choice. This allows a program to identify a color space for all images, which may be much easier and more reliable than trying to track the "unknown" color space. An ICC profile may be used; the ICC distributes three such profiles:[6] a profile conforming to version 4 of the ICC specification, which they recommend, and two profiles conforming to version 2, which is still commonly used.
Images intended for professional printing via a fully color-managed workflow, e.g. prepress output, sometimes use another color space such as Adobe RGB (1998), which allows for a wider gamut. If such images are to be used on the Internet they may be converted to sRGB using color management tools that are usually included with software that works in these other color spaces.
The two dominant programming interfaces for 3D graphics, OpenGL and Direct3D, have both incorporated half part support for the sRGB color space by using sRGB's gamma curve. OpenGL supports the textures with sRGB gamma encoded color components (first introduced with EXT_texture_sRGB extension, added to the core in OpenGL 2.1) and rendering into sRGB gamma encoded framebuffers (first introduced with EXT_framebuffer_sRGB extension, added to the core in OpenGL 3.0). Direct3D supports sRGB gamma textures and rendering into sRGB gamma surfaces starting with DirectX 9. Correct mipmapping and interpolation of sRGB gamma textures has direct hardware support in texturing units of most modern GPUs (for example nVidia GeForce 8 performs conversion from 8-bit texture to linear values before interpolating those values), and do not have any performance penalty.[7]
See also
References
- ↑ Charles A. Poynton (2003). Digital Video and HDTV: Algorithms and Interfaces. Morgan Kaufmann. ISBN 1-55860-792-7.
- ↑ 2.0 2.1 2.2 2.3 Michael Stokes, Matthew Anderson, Srinivasan Chandrasekar, Ricardo Motta (November 5, 1996). "A Standard Default Color Space for the Internet – sRGB, Version 1.10".
- ↑ Phil Green and Lindsay W. MacDonald (2002). Colour Engineering: Achieving Device Independent Colour. John Wiley and Sons. ISBN 0-471-48688-4.
- ↑ Jon Y. Hardeberg (2001). Acquisition and Reproduction of Color Images: Colorimetric and Multispectral Approaches. Universal-Publishers.com. ISBN 1-58112-135-0.
- ↑ Rodney, Andrew (2005). Color Management for Photographers. Focal Press. p. 121. ISBN 978-0-240-80649-5. "Why Calibrate Monitor to D65 When Light Booth is D50"
- ↑ sRGB profiles, ICC
- ↑ GPU Gems 3, section 24.4.1, http://http.developer.nvidia.com/GPUGems3/gpugems3_ch24.html
Standards
- IEC 61966-2-1:1999 is the official specification of sRGB. It provides viewing environment, encoding, and colorimetric details.
- Amendment A1:2003 to IEC 61966-2-1:1999 describes an analogous sYCC encoding for YCbCr color spaces, an extended-gamut RGB encoding, and a CIELAB transformation.
- sRGB on www.color.org
- The fourth working draft of IEC 61966-2-1 is available online, but is not the complete standard. It can be downloaded from www2.units.it.
External links
- International Color Consortium
- Archive copy of http://www.srgb.com, now unavailable, containing much information on the design, principles and use of sRGB
- A Standard Default Color Space for the Internet – sRGB at w3.org
- OpenGL extension for sRGB gamma textures at sgi.com
- Conversion matrices for RGB vs. XYZ conversion
- Will the Real sRGB Profile Please Stand Up?
| ||||||||||||||||||||