Runge–Kutta methods
In numerical analysis, the Runge–Kutta methods (German pronunciation: [ˌʁʊŋəˈkʊta]) are an important family of implicit and explicit iterative methods, which are used in temporal discretization for the approximation of solutions of ordinary differential equations. These techniques were developed around 1900 by the German mathematicians C. Runge and M. W. Kutta.
See the article on numerical methods for ordinary differential equations for more background and other methods. See also List of Runge–Kutta methods.
The Runge–Kutta method
One member of the family of Runge–Kutta methods is often referred to as "RK4", "classical Runge–Kutta method" or simply as "the Runge–Kutta method".
Let an initial value problem be specified as follows.
Here, y is an unknown function (scalar or vector) of time t which we would like to approximate; we are told that 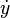 , the rate at which y changes, is a function of t and of y itself. At the initial time
, the rate at which y changes, is a function of t and of y itself. At the initial time  the corresponding y-value is
the corresponding y-value is  . The function f and the data
. The function f and the data  ,
,  are given.
are given.
Now pick a step-size h>0 and define
for n = 0, 1, 2, 3, . . . , using
Here 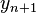 is the RK4 approximation of
is the RK4 approximation of  , and the next value (
, and the next value (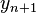 ) is determined by the present value (
) is determined by the present value ( ) plus the weighted average of four increments, where each increment is the product of the size of the interval, h, and an estimated slope specified by function f on the right-hand side of the differential equation.
) plus the weighted average of four increments, where each increment is the product of the size of the interval, h, and an estimated slope specified by function f on the right-hand side of the differential equation.
-
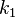 is the increment based on the slope at the beginning of the interval, using
is the increment based on the slope at the beginning of the interval, using 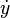 , (Euler's method) ;
, (Euler's method) ; -
 is the increment based on the slope at the midpoint of the interval, using
is the increment based on the slope at the midpoint of the interval, using  ;
; -
 is again the increment based on the slope at the midpoint, but now using
is again the increment based on the slope at the midpoint, but now using 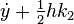 ;
; -
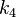 is the increment based on the slope at the end of the interval, using
is the increment based on the slope at the end of the interval, using  .
.
In averaging the four increments, greater weight is given to the increments at the midpoint. The weights are chosen such that if  is independent of
is independent of  , so that the differential equation is equivalent to a simple integral, then RK4 is Simpson's rule.[3]
, so that the differential equation is equivalent to a simple integral, then RK4 is Simpson's rule.[3]
The RK4 method is a fourth-order method, meaning that the local truncation error is on the order of  , while the total accumulated error is order
, while the total accumulated error is order 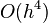 .
.
Tan Delin and Chen Zheng have developed a general formula for Runge-Kutta method in fourth-order as the following.
for n = 0, 1, 2, 3, . . . , using
Where 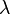 is a free parameter. Choosing
is a free parameter. Choosing 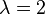 , this is the classical fourth-order Runge-Kutta method. With
, this is the classical fourth-order Runge-Kutta method. With 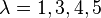 , this formula produces other fourth-order Runge-Kutta methods.
, this formula produces other fourth-order Runge-Kutta methods.
Explicit Runge–Kutta methods
The family of explicit Runge–Kutta methods is a generalization of the RK4 method mentioned above. It is given by
where
To specify a particular method, one needs to provide the integer s (the number of stages), and the coefficients aij (for 1 ≤ j < i ≤ s), bi (for i = 1, 2, ..., s) and ci (for i = 2, 3, ..., s). The matrix [aij] is called the Runge–Kutta matrix, while the bi and ci are known as the weights and the nodes.[5] These data are usually arranged in a mnemonic device, known as a Butcher tableau (after John C. Butcher):
| 0 | ||||||
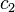 | 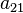 | |||||
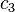 |  | 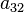 | ||||
 |  | 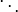 | ||||
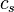 |
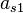 |
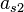 |
 |
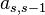 | ||
 | 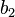 |  |  | 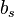 |
The Runge–Kutta method is consistent if
There are also accompanying requirements if we require the method to have a certain order p, meaning that the local truncation error is O(hp+1). These can be derived from the definition of the truncation error itself. For example, a 2-stage method has order 2 if b1 + b2 = 1, b2c2 = 1/2, and a21 = c2.[6]
Examples
The RK4 method falls in this framework. Its tableau is:[7]
| 0 | |||||
| 1/2 | 1/2 | ||||
| 1/2 | 0 | 1/2 | |||
| 1 | 0 | 0 | 1 | ||
| 1/6 | 1/3 | 1/3 | 1/6 |
A slight variation of "the" Runge-Kutta method is also due to Kutta in 1901 and is called the 3/8-rule.[8] The primary advantage this method has is that almost all of the error coefficients are smaller than the popular method, but it requires slightly more FLOPs (floating point operations) per time step. Its Butcher tableau is given by:
| 0 | |||||
| 1/3 | 1/3 | ||||
| 2/3 | −1/3 | 1 | |||
| 1 | 1 | −1 | 1 | ||
| 1/8 | 3/8 | 3/8 | 1/8 |
However, the simplest Runge–Kutta method is the (forward) Euler method, given by the formula 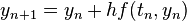 . This is the only consistent explicit Runge–Kutta method with one stage. The corresponding tableau is:
. This is the only consistent explicit Runge–Kutta method with one stage. The corresponding tableau is:
| 0 | ||
| 1 |
Second-order methods with two stages
An example of a second-order method with two stages is provided by the midpoint method
The corresponding tableau is:
| 0 | |||
| 1/2 | 1/2 | ||
| 0 | 1 |
The midpoint method is not the only second-order Runge–Kutta method with two stages. In fact, there is a family of such methods, parameterized by α, and given by the formula
Its Butcher tableau is
| 0 | |||
 |  | ||
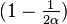 |  |
In this family,  gives the midpoint method and
gives the midpoint method and 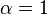 is Heun's method.[3]
is Heun's method.[3]
Usage
As an example, consider the two-stage second-order Runge–Kutta method with α = 2/3. It is given by the tableau
| 0 | |||
| 2/3 | 2/3 | ||
| 1/4 | 3/4 |
with the corresponding equations
This method is used to solve the initial-value problem
with step size h = 0.025, so the method needs to take four steps.
The method proceeds as follows:
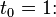 | |||
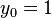 | |||
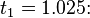 | |||
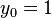 | 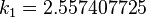 | 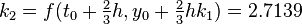 | |
 | |||
 | |||
 | 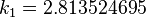 | 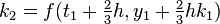 | |
 | |||
 | |||
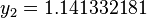 | 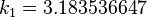 | 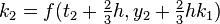 | |
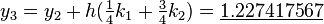 | |||
 | |||
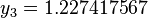 | 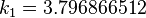 | 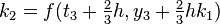 | |
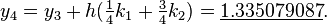 | |||
The numerical solutions correspond to the underlined values.
Adaptive Runge–Kutta methods
The adaptive methods are designed to produce an estimate of the local truncation error of a single Runge–Kutta step. This is done by having two methods in the tableau, one with order  and one with order
and one with order  .
.
The lower-order step is given by
where the  are the same as for the higher-order method. Then the error is
are the same as for the higher-order method. Then the error is
which is 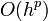 .
The Butcher tableau for this kind of method is extended to give the values of
.
The Butcher tableau for this kind of method is extended to give the values of  :
:
| 0 | ||||||
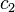 | 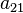 | |||||
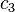 |  | 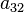 | ||||
 |  |  | ||||
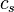 |
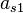 |
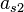 |
 |
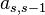 | ||
 | 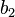 |  |  | 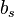 | ||
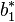 | 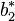 |  |  | 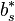 |
The Runge–Kutta–Fehlberg method has two methods of orders 5 and 4. Its extended Butcher tableau is:
| 0 | |||||||
| 1/4 | 1/4 | ||||||
| 3/8 | 3/32 | 9/32 | |||||
| 12/13 | 1932/2197 | −7200/2197 | 7296/2197 | ||||
| 1 | 439/216 | −8 | 3680/513 | -845/4104 | |||
| 1/2 | −8/27 | 2 | −3544/2565 | 1859/4104 | −11/40 | ||
| 16/135 | 0 | 6656/12825 | 28561/56430 | −9/50 | 2/55 | ||
| 25/216 | 0 | 1408/2565 | 2197/4104 | −1/5 | 0 |
However, the simplest adaptive Runge–Kutta method involves combining the Heun method, which is order 2, with the Euler method, which is order 1. Its extended Butcher tableau is:
| 0 | |||
| 1 | 1 | ||
| 1/2 | 1/2 | ||
| 1 | 0 |
The error estimate is used to control the stepsize.
Other adaptive Runge–Kutta methods are the Bogacki–Shampine method (orders 3 and 2), the Cash–Karp method and the Dormand–Prince method (both with orders 5 and 4).
Nonconfluent Runge-Kutta methods
A Runge-Kutta method is said to be nonconfluent [10] if all the 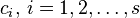 are distinct.
are distinct.
Implicit Runge–Kutta methods
All Runge–Kutta methods mentioned up to now are explicit methods. Unfortunately, explicit Runge–Kutta methods are generally unsuitable for the solution of stiff equations because their region of absolute stability is small; in particular, it is bounded.[11] This issue is especially important in the solution of partial differential equations.
The instability of explicit Runge–Kutta methods motivates the development of implicit methods. An implicit Runge–Kutta method has the form
where
The difference with an explicit method is that in an explicit method, the sum over j only goes up to i − 1. This also shows up in the Butcher tableau. For an implicit method, the coefficient matrix 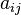 is not necessarily lower triangular:[7]
is not necessarily lower triangular:[7]
The consequence of this difference is that at every step, a system of algebraic equations has to be solved. This increases the computational cost considerably. If a method with s stages is used to solve a differential equation with m components, then the system of algebraic equations has ms components. In contrast, an implicit s-step linear multistep method needs to solve a system of algebraic equations with only s components.[13]
Examples
The simplest example of an implicit Runge–Kutta method is the backward Euler method:
The Butcher tableau for this is simply:
This Butcher tableau corresponds to the formulae
which can be re-arranged to get the formula for the backward Euler method listed above.
Another example for an implicit Runge–Kutta method is the trapezoidal rule. Its Butcher tableau is:
The trapezoidal rule is a collocation method (as discussed in that article). All collocation methods are implicit Runge–Kutta methods, but not all implicit Runge–Kutta methods are collocation methods.[14]
The Gauss–Legendre methods form a family of collocation methods based on Gauss quadrature. A Gauss–Legendre method with s stages has order 2s (thus, methods with arbitrarily high order can be constructed).[15] The method with two stages (and thus order four) has Butcher tableau:
Stability
The advantage of implicit Runge–Kutta methods above explicit ones is their greater stability, especially when applied to stiff equations. Consider the linear test equation y' = λy. A Runge–Kutta method applied to this equation reduces to the iteration 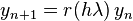 , with r given by
, with r given by
where e stands for the vector of ones. The function r is called the stability function.[17] It follows from the formula that r is the quotient of two polynomials of degree s if the method has s stages. Explicit methods have a strictly lower triangular matrix A, which implies that det(I − zA) = 1 and that the stability function is a polynomial.[18]
The numerical solution to the linear test equation decays to zero if | r(z) | < 1 with z = hλ. The set of such z is called the domain of absolute stability. In particular, the method is said to be A-stable if all z with Re(z) < 0 are in the domain of absolute stability. The stability function of an explicit Runge–Kutta method is a polynomial, so explicit Runge–Kutta methods can never be A-stable.[18]
If the method has order p, then the stability function satisfies 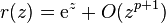 as
as  . Thus, it is of interest to study quotients of polynomial of given degrees that approximate the exponential function the best. These are known as Padé approximants. A Padé approximant with numerator of degree m and denominator of degree n is A-stable if and only if m ≤ n ≤ m + 2.[19]
. Thus, it is of interest to study quotients of polynomial of given degrees that approximate the exponential function the best. These are known as Padé approximants. A Padé approximant with numerator of degree m and denominator of degree n is A-stable if and only if m ≤ n ≤ m + 2.[19]
The Gauss–Legendre method with s stages has order 2s, so its stability function is the Padé approximant with m = n = s. It follows that the method is A-stable.[20] This shows that A-stable Runge–Kutta can have arbitrarily high order. In contrast, the order of A-stable linear multistep methods cannot exceed two.[21]
B-stability. Algebraic stability
The A-stability concept for the solution of differential equations is related to the linear autonomous equation  . Dahlquist proposed the investigation of stability of numerical schemes when applied to nonlinear systems which satisfies a monotonicity condition. The corresponding concepts were defined as G-stability for multistep methods (and the related one-leg methods) and B-stability (Butcher, 1975) for Runge-Kutta methods. A Runge-Kutta method applied to the non-linear system
. Dahlquist proposed the investigation of stability of numerical schemes when applied to nonlinear systems which satisfies a monotonicity condition. The corresponding concepts were defined as G-stability for multistep methods (and the related one-leg methods) and B-stability (Butcher, 1975) for Runge-Kutta methods. A Runge-Kutta method applied to the non-linear system 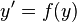 , which verifies
, which verifies 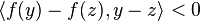 , is called B-stable, if this condition implies
, is called B-stable, if this condition implies 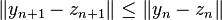 for two numerical solutions.
for two numerical solutions.
Let  ,
,  and
and  three
three  matrices defined by
matrices defined by
A Runge-Kutta method is said to be algebraically stable [22] if the matrices both  and
and  are both non-negative definite. A sufficient condition for B-stability [23] is:
are both non-negative definite. A sufficient condition for B-stability [23] is:  and
and  are non-negative definite.
are non-negative definite.
Derivation of the Runge–Kutta fourth-order method
In general a Runge–Kutta method of order  can be written as:
can be written as:
where:
are increments obtained evaluating the derivatives of 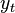 at the
at the  -th order.
-th order.
We develop the derivation[24] for the Runge–Kutta fourth-order method using the general formula with 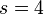 evaluated, as explained above, at the starting point, the midpoint and the end point of any interval
evaluated, as explained above, at the starting point, the midpoint and the end point of any interval 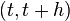 , thus we choose:
, thus we choose:
and 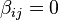 otherwise. We begin by defining the following quantities:
otherwise. We begin by defining the following quantities:
 :
: :
:
where 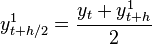 and
and 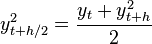 If we define:
If we define:
 :
: :
: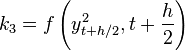 :
: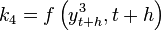
and for the previous relations we can show that the following equalities holds up to  :
:
where:
is the total derivative of  with respect to time.
with respect to time.
If we now express the general formula using what we just derived we obtain:
and comparing this with the Taylor series of  around
around 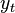 :
:
we obtain a system of constraints on the coefficients:
which solved gives  as stated above.
as stated above.
See also
- Dynamic errors of numerical methods of ODE discretization
- Euler's method
- List of Runge–Kutta methods
- Numerical ordinary differential equations
- Runge–Kutta method (SDE)
Notes
- ↑ Press et al. 2007, p. 908; Süli & Mayers 2003, p. 328
- ↑ 2.0 2.1 Atkinson (1989, p. 423), Hairer, Nørsett & Wanner (1993, p. 134), Kaw & Kalu (2008, §8.4) and Stoer & Bulirsch (2002, p. 476) leave out the factor h in the definition of the stages. Ascher & Petzold (1998, p. 81), Butcher (2003, p. 93) and Iserles (1996, p. 38) use the y-values as stages.
- ↑ 3.0 3.1 Süli & Mayers 2003, p. 328
- ↑ Press et al. 2007, p. 907
- ↑ Iserles 1996, p. 38
- ↑ Iserles 1996, p. 39
- ↑ 7.0 7.1 Süli & Mayers 2003, p. 352
- ↑ Hairer, Nørsett & Wanner (1993, p. 138) refer to Kutta (1901)
- ↑ Süli & Mayers 2003, p. 327
- ↑ Lambert 1991, p. 278
- ↑ Süli & Mayers 2003, pp. 349–351
- ↑ Iserles 1996, p. 41; Süli & Mayers 2003, pp. 351–352
- ↑ 13.0 13.1 Süli & Mayers 2003, p. 353
- ↑ Iserles 1996, pp. 43–44
- ↑ Iserles 1996, p. 47
- ↑ Hairer & Wanner 1996, pp. 40–41
- ↑ Hairer & Wanner 1996, p. 40
- ↑ 18.0 18.1 Iserles 1996, p. 60
- ↑ Iserles 1996, pp. 62–63
- ↑ Iserles 1996, p. 63
- ↑ This result is due to Dahlquist (1963).
- ↑ Lambert 1991, p. 275
- ↑ Lambert 1991, p. 274
- ↑ PDF reporting this derivation
References
- Ascher, Uri M.; Petzold, Linda R. (1998), Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations, Philadelphia: Society for Industrial and Applied Mathematics, ISBN 978-0-89871-412-8.
- Atkinson, Kendall A. (1989), An Introduction to Numerical Analysis (2nd ed.), New York: John Wiley & Sons, ISBN 978-0-471-50023-0.
- Butcher, John C. (May 1963), "Coefficients for the study of Runge-Kutta integration processes" 3 (2), pp. 185–201, doi:10.1017/S1446788700027932.
- Butcher, John C. (1975), "A stability property of implicit Runge-Kutta methods", BIT 15: 358–361.
- Butcher, John C. (2003), Numerical Methods for Ordinary Differential Equations, New York: John Wiley & Sons, ISBN 978-0-471-96758-3.
- Cellier, F.; Kofman, E. (2006), Continuous System Simulation, Springer Verlag, ISBN 0-387-26102-8.
- Dahlquist, Germund (1963), "A special stability problem for linear multistep methods", BIT 3: 27–43, doi:10.1007/BF01963532, ISSN 0006-3835.
- Forsythe, George E.; Malcolm, Michael A.; Moler, Cleve B. (1977), Computer Methods for Mathematical Computations, Prentice-Hall (see Chapter 6).
- Hairer, Ernst; Nørsett, Syvert Paul; Wanner, Gerhard (1993), Solving ordinary differential equations I: Nonstiff problems, Berlin, New York: Springer-Verlag, ISBN 978-3-540-56670-0.
- Hairer, Ernst; Wanner, Gerhard (1996), Solving ordinary differential equations II: Stiff and differential-algebraic problems (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-60452-5.
- Iserles, Arieh (1996), A First Course in the Numerical Analysis of Differential Equations, Cambridge University Press, ISBN 978-0-521-55655-2.
- Lambert, J.D (1991), Numerical Methods for Ordinary Differential Systems. The Initial Value Problem, John Wiley & Sons, ISBN 0-471-92990-5
- Kaw, Autar; Kalu, Egwu (2008), Numerical Methods with Applications (1st ed.), autarkaw.com.
- Kutta, Martin Wilhelm (1901), "Beitrag zur näherungsweisen Integration totaler Differentialgleichungen", Zeitschrift für Mathematik und Physik 46: 435–453.
- Press, William H.; Flannery, Brian P.; Teukolsky, Saul A.; Vetterling, William T. (2007), "Section 17.1 Runge-Kutta Method", Numerical Recipes: The Art of Scientific Computing (3rd ed.), Cambridge University Press, ISBN 978-0-521-88068-8. Also, Section 17.2. Adaptive Stepsize Control for Runge-Kutta.
- Stoer, Josef; Bulirsch, Roland (2002), Introduction to Numerical Analysis (3rd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-95452-3.
- Süli, Endre; Mayers, David (2003), An Introduction to Numerical Analysis, Cambridge University Press, ISBN 0-521-00794-1.
- Tan, Delin; Chen, Zheng (2012), "On A General Formula of Fourth Order Runge-Kutta Method", Journal of Mathematical Science & Mathematics Education 7.2: 1–10.
External links
- Hazewinkel, Michiel, ed. (2001), "Runge-Kutta method", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Runge–Kutta 4th-Order Method
- Runge Kutta Method for O.D.E.'s
- DotNumerics: Ordinary Differential Equations for C# and VB.NET — Initial-value problem for nonstiff and stiff ordinary differential equations (explicit Runge–Kutta, implicit Runge–Kutta, Gear's BDF and Adams–Moulton).
- GafferOnGames — A physics resource for computer programmers
- PottersWheel — Parameter calibration in ODE systems using implicit Runge–Kutta integration
| |||||||||||
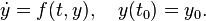
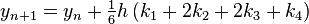
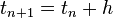
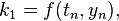
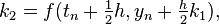

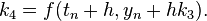
![y_{{n+1}}=y_{n}+{\tfrac {1}{6}}h\left[k_{1}+\left(4-\lambda \right)k_{2}+\lambda k_{3}+k_{4}\right]](/2014-wikipedia_en_all_02_2014/I/media/e/4/7/f/e47f2aa0cfe7a7a118f029a72b2649b5.png)
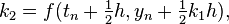
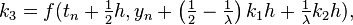
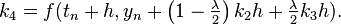




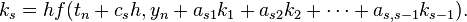

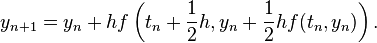
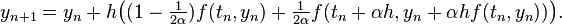
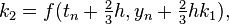
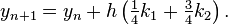
![y'=\tan(y)+1,\quad y_{0}=1,\ t\in [1,1.1]](/2014-wikipedia_en_all_02_2014/I/media/7/9/9/8/79987d68035565eabf4be46bc33d7be9.png)




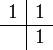
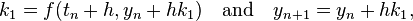



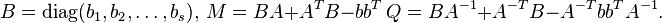
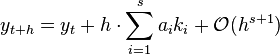

![{\begin{array}{|l|l|}\hline \alpha _{i}&\beta _{{ij}}\\[8pt]\hline \alpha _{1}=0&\beta _{{21}}={\frac {1}{2}}\\[8pt]\alpha _{2}={\frac {1}{2}}&\beta _{{32}}={\frac {1}{2}}\\[8pt]\alpha _{3}={\frac {1}{2}}&\beta _{{43}}=1\\[8pt]\alpha _{4}=1&\\[8pt]\hline \end{array}}](/2014-wikipedia_en_all_02_2014/I/media/b/b/8/d/bb8dbd687bf1ef881ff957bfca71ea07.png)
![{\begin{array}{ll}k_{2}&=f\left(y_{{t+h/2}}^{1},t+{\frac {h}{2}}\right)=f\left(y_{t}+{\frac {h}{2}}k_{1},t+{\frac {h}{2}}\right)\\&=f\left(y_{t},t\right)+{\frac {h}{2}}{\frac {d}{dt}}f\left(y_{t},t\right)\\k_{3}&=f\left(y_{{t+h/2}}^{2},t+{\frac {h}{2}}\right)=f\left(y_{t}+{\frac {h}{2}}f\left(y_{t}+{\frac {h}{2}}k_{1},t+{\frac {h}{2}}\right),t+{\frac {h}{2}}\right)\\&=f\left(y_{t},t\right)+{\frac {h}{2}}{\frac {d}{dt}}\left[f\left(y_{t},t\right)+{\frac {h}{2}}{\frac {d}{dt}}f\left(y_{t},t\right)\right]\\k_{4}&=f\left(y_{{t+h}}^{3},t+h\right)=f\left(y_{t}+hf\left(y_{t}+{\frac {h}{2}}k_{2},t+{\frac {h}{2}}\right),t+h\right)\\&=f\left(y_{t}+hf\left(y_{t}+{\frac {h}{2}}f\left(y_{t}+{\frac {h}{2}}f\left(y_{t},t\right),t+{\frac {h}{2}}\right),t+{\frac {h}{2}}\right),t+h\right)\\&=f\left(y_{t},t\right)+h{\frac {d}{dt}}\left[f\left(y_{t},t\right)+{\frac {h}{2}}{\frac {d}{dt}}\left[f\left(y_{t},t\right)+{\frac {h}{2}}{\frac {d}{dt}}f\left(y_{t},t\right)\right]\right]\end{array}}](/2014-wikipedia_en_all_02_2014/I/media/8/a/f/b/8afbb1ab805f3b53b9caf55e9735fbb3.png)
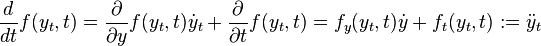
![{\begin{array}{ll}y_{{t+h}}&=y_{t}+h\left\lbrace a\cdot f(y_{t},t)+b\cdot \left[f\left(y_{t},t\right)+{\frac {h}{2}}{\frac {d}{dt}}f\left(y_{t},t\right)\right]\right.+\\&{}+c\cdot \left[f\left(y_{t},t\right)+{\frac {h}{2}}{\frac {d}{dt}}\left[f\left(y_{t},t\right)+{\frac {h}{2}}{\frac {d}{dt}}f\left(y_{t},t\right)\right]\right]+\\&{}+d\cdot \left[f\left(y_{t},t\right)+h{\frac {d}{dt}}\left[f\left(y_{t},t\right)+{\frac {h}{2}}{\frac {d}{dt}}\left[f\left(y_{t},t\right)+\left.{\frac {h}{2}}{\frac {d}{dt}}f\left(y_{t},t\right)\right]\right]\right]\right\rbrace +{\mathcal {O}}(h^{5})\\&=y_{t}+a\cdot hf_{t}+b\cdot hf_{t}+b\cdot {\frac {h^{2}}{2}}{\frac {df_{t}}{dt}}+c\cdot hf_{t}+c\cdot {\frac {h^{2}}{2}}{\frac {df_{t}}{dt}}+\\&{}+c\cdot {\frac {h^{3}}{4}}{\frac {d^{2}f_{t}}{dt^{2}}}+d\cdot hf_{t}+d\cdot h^{2}{\frac {df_{t}}{dt}}+d\cdot {\frac {h^{3}}{2}}{\frac {d^{2}f_{t}}{dt^{2}}}+d\cdot {\frac {h^{4}}{4}}{\frac {d^{3}f_{t}}{dt^{3}}}+{\mathcal {O}}(h^{5})\end{array}}](/2014-wikipedia_en_all_02_2014/I/media/1/9/d/b/19db2d3fc854568f6d934f05c7e4e25d.png)

![{\begin{cases}&a+b+c+d=1\\[6pt]&{\frac {1}{2}}b+{\frac {1}{2}}c+d={\frac {1}{2}}\\[6pt]&{\frac {1}{4}}c+{\frac {1}{2}}d={\frac {1}{6}}\\[6pt]&{\frac {1}{4}}d={\frac {1}{24}}\end{cases}}](/2014-wikipedia_en_all_02_2014/I/media/7/5/7/8/75782b7fa0d332a0c0985e4851d573ad.png)