Runcicantic cubic honeycomb
From Wikipedia, the free encyclopedia
| Runcicantic cubic honeycomb | |
|---|---|
  | |
| Type | Uniform honeycomb |
| Schläfli symbol | h2,3{4,3,4} |
| Coxeter-Dynkin diagrams | |
| Coxeter group | 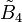 , [4,31,1] , [4,31,1] |
| Vertex figure |  |
| Dual | half pyramidille |
| Symmetry group | Fm3m (225) |
| Properties | vertex-transitive |
The runcicantic cubic honeycomb is a uniform space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of truncated cuboctahedra, truncated cubes and truncated tetrahedra in a ratio of 1:1:2. It is related to the runcicantellated cubic honeycomb.
John Horton Conway calls this honeycomb a f-tCO-trille, and its dual half pyramidille.
Images
 Runcicantic cubic |
 Runcicantellated cubic |
Related honeycombs
| Space group |
Fibrifold | Extended symmetry |
Extended diagram |
Order | Honeycombs |
|---|---|---|---|---|---|
| Pm3m (221) |
4−:2 | [4,3,4] | ×1 | ||
| Fm3m (225) |
2−:2 | [1+,4,3,4] = [4,31,1] |
= |
Half | |
| I43m (217) |
4o:2 | [[(4,3,4,2+)]] | Half × 2 | ||
| Fd3m (227) |
2+:2 | [[1+,4,3,4,1+]] = [[3[4]]] |
= |
Quarter × 2 | |
| Im3m (229) |
8o:2 | [[4,3,4]] | ×2 |
The [4,31,1], ![]()
![]()
![]()
![]()
![]() , Coxeter group generates 9 permutations of uniform tessellations, 4 with distinct geometry including the alternated cubic honeycomb.
, Coxeter group generates 9 permutations of uniform tessellations, 4 with distinct geometry including the alternated cubic honeycomb.
| Space group |
Fibrifold | Extended symmetry |
Extended diagram |
Order | Honeycombs |
|---|---|---|---|---|---|
| Fm3m (225) |
2−:2 | [4,31,1] = [4,3,4,1+] |
= |
×1 | |
| Fm3m (225) |
2−:2 | <[1+,4,31,1]> = <[3[4]]> |
= |
×2 | |
| Pm3m (221) |
4−:2 | <[4,31,1]> | ×2 |
See also
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, Architectonic and Catoptric tessellations, p 292-298, includes all the nonprismatic forms)
- George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
- Branko Grünbaum, Uniform tilings of 3-space. Geombinatorics 4(1994), 49 - 56.
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X.
- Critchlow, Keith (1970). Order in Space: A design source book. Viking Press. ISBN 0-500-34033-1.
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Uniform space-fillings)
- A. Andreini, Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative (On the regular and semiregular nets of polyhedra and on the corresponding correlative nets), Mem. Società Italiana della Scienze, Ser.3, 14 (1905) 75–129.
- D. M. Y. Sommerville, An Introduction to the Geometry of n Dimensions. New York, E. P. Dutton, 1930. 196 pp. (Dover Publications edition, 1958) Chapter X: The Regular Polytopes
- Richard Klitzing, 3D Euclidean Honeycombs, x3x3o *b4x - gratoh - O28
- Uniform Honeycombs in 3-Space: 14-Gratoh
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.