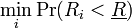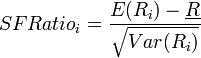Roy's safety-first criterion

From Wikipedia, the free encyclopedia

Roy's safety-first criterion is a risk management technique that allows an investor to select one portfolio rather than another based on the criterion that the probability of the portfolio's return falling below a minimum desired threshold is minimized.[1]

For example, suppose there are two available investment strategies - portfolio A and portfolio B, and suppose the investor's threshold return level (the minimum return that the investor is willing to tolerate) is -1%. then the investor would choose the portfolio that would provide the maximum probability of the portfolio return being at least as high as −1%.

Thus, the problem of an investor using Roy's safety criterion can be summarized symbolically as:

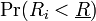{\underset {i}{\min }}\Pr(R_{{i}}<\underline {R})

where \Pr(R_{{i}}<\underline {R}) is the probability of 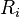R_{{i}} (the actual return of asset i) being less than 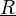\underline {R} (the minimum acceptable return).

Normally distributed return and SFRatio

If the portfolios under consideration have normally distributed returns, Roy's safety-first criterion can be reduced to the maximization of the safety-first ratio, defined by:

SFRatio_{{i}}={\frac {E(R_{{i}})-\underline {R}}{{\sqrt {Var(R_{{i}})}}}}

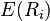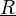where E(R_{{i}}) is the expected return (the mean return) of the portfolio, {\sqrt {Var(R_{{i}})}} is the standard deviation of the portfolio's return and \underline {R} is the minimum acceptable return.

Example

If Portfolio A has an expected return of 10% and standard deviation of 15%, while portfolio B has a mean return of 8% and a standard deviation of 5%, and the investor is willing to invest in a portfolio that maximizes the probability of a return no lower than 0%:

SFRatio(A) = [10 − 0]/15 = 0.67,
SFRatio(B) = [8 − 0]/5 = 1.6

By Roy's safety-first criterion, the investor would choose portfolio B as the correct investment opportunity.

Similarity to Sharpe Ratio

Under normality,

SFRatio = (expected return − minimum return)/(standard deviation of return).

Recall that Sharpe ratio is defined as excess return per unit of risk, or in other words:

Sharpe ratio = [Expected return − Risk-Free Return]/(standard deviation of [Expected return − Risk-Free Return]).

SFRatio has a striking similarity to Sharpe ratio. Thus for normally distributed returns, Roy's Safety-first criterion - with the minimum return equal to the risk-free rate - provides the same conclusions (about which portfolio to invest in) as if we were picking the one with the maximum Sharpe Ratio.

See also

  • Value at Risk

References

  1. ↑ Roy, Arthur D. (1952). "Safety First and the Holding of Assets". Econometrica 1952 (July): 431–450. 
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.